已知:0°<α<90°,0°<α+β<90°,3sinβ=sin(2α+β),则tanβ的最大值是 .
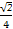
【解析】由3sinβ=sin(2α+β)得3sin(α+β-α)=sin(α+β+α),化简得sin(α+β)cosα=2cos(α+β)sinα,
∴tan(α+β)=2tanα,
∴tanβ=tan(α+β-α)=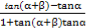
=
=
.
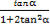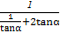由题意知,tanα>0,
∴
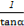+2tanα≥2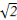
(当且仅当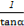=2tanα,即tanα=
时等号成立),
∴tanβ的最大值为
=.
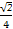【方法技巧】三角函数和差公式的灵活应用
(1)三角函数和差公式在三角函数式的化简和求值中经常用到,因此公式的灵活应用非常关键,公式可以正用、逆用、变形应用.
(2)逆用关键在于构造公式的形式,方法是通过三角恒等变换,出现和或差的形式,即出现能逆用公式的条件;有时通过两式平方相加减,利用平方关系式,切函数化成弦函数等技巧.
科目：高中数学 来源：2014年高考数学全程总复习课时提升作业二十五第四章第一节练习卷（解析版） 题型：选择题
设a,b是非零向量,则下列不等式中不恒成立的是( )
(A)|a+b|≤|a|+|b|(B)|a|-|b|≤|a+b|
(C)|a|-|b|≤|a|+|b|(D)|a|≤|a+b|
查看答案和解析>>
科目：高中数学 来源：2014年高考数学全程总复习课时提升作业二十七第四章第三节练习卷（解析版） 题型：选择题
设a,b是不共线的两个向量,其夹角是θ,若函数f(x)=(xa+b)·(a-xb)(x∈R)在(0,+∞)上有最大值,则( )
(A)|a|<|b|,且θ是钝角
(B)|a|<|b|,且θ是锐角
(C)|a|>|b|,且θ是钝角
(D)|a|>|b|,且θ是锐角
查看答案和解析>>
科目：高中数学 来源：2014年高考数学全程总复习课时提升作业二十七第四章第三节练习卷（解析版） 题型：选择题
有下列四个命题:
①(a·b)2=a2·b2;②|a+b|>|a-b|;③|a+b|2=(a+b)2;④若a∥b,则a·b=|a|·|b|.其中真命题的个数是( )
(A)1 (B)2 (C)3 (D)4
查看答案和解析>>
科目：高中数学 来源：2014年高考数学全程总复习课时提升作业二十一第三章第五节练习卷（解析版） 题型：选择题
已知向量a=(sin(α+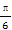
),1),b=(4,4cosα-
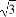),若a⊥b,则sin(α+
)=( )
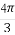(A)-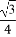
(B)-
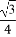(C) (D)
查看答案和解析>>
科目：高中数学 来源：2014年高考数学全程总复习课时提升作业三十第五章第一节练习卷（解析版） 题型：解答题
已知数列{an}的前n项和为Sn,若S1=1,S2=2,且Sn+1-3Sn+2Sn-1=0(n∈N*且n≥2),求该数列的通项公式.
查看答案和解析>>
科目：高中数学 来源：2014年高考数学全程总复习课时提升作业三十四第五章第五节练习卷（解析版） 题型：解答题
设函数f(x)=
+sinx的所有正的极小值点从小到大排成的数列为{xn}.
(1)求数列{xn}的通项公式.
(2)设{xn}的前n项和为Sn,求sinSn.
查看答案和解析>>
科目：高中数学 来源：2014年高考数学全程总复习课时提升作业三十八第六章第四节练习卷（解析版） 题型：选择题
某公司一年购买某种货物400吨,每次都购买x吨,运费为4万元/次,一年的总存储费用为4x万元,要使一年的总运费与总存储费用之和最小,则x=( )
(A)20 (B)10 (C)16 (D)8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
