
分析 若“p或q”为真,“p且q”为假,则命题p,q一真一假;分类讨论得到不同情况下c的取值,综合可得答案.
解答 解:若命题p:函数y=cx在R上单调递减,为真命题,
则c∈(0,1);
若命题q:函数f(x)=x2-cx的最小值小于-$\frac{1}{16}$,为真命题,
$\frac{-{c}^{2}}{4}$<-$\frac{1}{16}$,
解得:c∈($\frac{1}{2}$,+∞),
∵“p或q”为真,“p且q”为假,
∴命题p,q一真一假;
p真q假时,c∈(0,$\frac{1}{2}$],
p假q真时,c∈[1,+∞),
综上可得:c∈(0,$\frac{1}{2}$]∪[1,+∞)
点评 本题以命题的真假判断与应用为载体,考查了复合命题,指数函数的单调性,二次函数的图象和性质等知识点,难度中档.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届山东临沭一中高三上学期10月月考数学(文)试卷(解析版) 题型:解答题
已知定义域为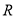 的函数
的函数 是奇函数.
是奇函数.
(1)求 ,
,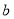 的值;
的值;
(2)用定义证明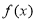 在
在 上为减函数;
上为减函数;
(3)若对于任意 ,不等式
,不等式 恒成立,求
恒成立,求 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[0,\frac{{\sqrt{3}}}{3}]$ | B. | $[0,\sqrt{3}]$ | C. | $[\sqrt{3}-1,\sqrt{3}]$ | D. | $[\frac{{\sqrt{3}-1}}{2},\sqrt{3}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com