
【题目】已知:函数f(x)=loga(2+x)-loga(2-x)(a>0且a≠1)
(Ⅰ)求f(x)定义域;
(Ⅱ)判断f(x)的奇偶性,并说明理由;
(Ⅲ)求使f(x)>0的x的解集.
【答案】(Ⅰ){x|-2<x<2}(Ⅱ)奇函数(Ⅲ)当a>1时,不等式解集为(0,2);当0<a<1时,不等式解集为(-2,0)
【解析】
试题分析:(Ⅰ)函数定义域需满足对数的真数为正数;(Ⅱ)判断奇偶性需在定义域对称的基础上判断![]() 的关系;(Ⅲ)解不等式时对a分情况讨论,利用对数函数的单调性得到关于x的不等式,从而求其解集
的关系;(Ⅲ)解不等式时对a分情况讨论,利用对数函数的单调性得到关于x的不等式,从而求其解集
试题解析:(Ⅰ)解:∵f(x)=loga(2+x)-loga(2-x)(a>0且a≠1)
∴![]() ,
,
解得-2<x<2,
故所求函数f(x)的定义域为{x|-2<x<2}.
(Ⅱ)f(-x)=loga(-x+2)-loga(2+x)=-[loga(x+2)-loga(2-x)]=-f(x),
故f(x)为奇函数.
(Ⅲ)原不等式可化为:loga(2+x)>loga(2-x)
①当a>1时,y=logax单调递增,
∴![]()
即0<x<2,
②当0<a<1时,y=logax单调递减,
∴![]()
即-2<x<0,
综上所述:当a>1时,不等式解集为(0,2);当0<a<1时,不等式解集为(-2,0)


科目:高中数学 来源: 题型:
【题目】如图,正四棱锥![]() 中底面边长为
中底面边长为![]() ,侧棱
,侧棱![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() .
.
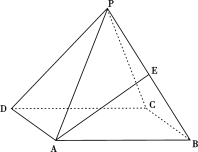
(1)求正四棱锥![]() 的外接球半径;
的外接球半径;
(2)若E是PB中点,求异面直线PD与AE所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() .
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某篮球比赛中,根据甲和乙两人的得分情况得到如图所示的茎叶图.

(1)从茎叶图的特征来说明他们谁发挥得更稳定;
(2)用样本的数字特征验证他们谁发挥得更好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线
)的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线![]() :
:![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() .
.
(1)求椭圆![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(2)设![]() 为坐标原点,直线
为坐标原点,直线![]() 平行于
平行于![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且与直线
,且与直线![]() 交于点
交于点![]() .证明:存在实数
.证明:存在实数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com