
【题目】如图,已知四棱锥![]() 的底面为直角梯形,
的底面为直角梯形, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() .
.
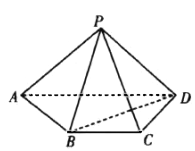
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)取![]() ,
, ![]() 的中点
的中点![]() ,
, ![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,
, ![]() ,可得
,可得![]() ,
, ![]() ,故得
,故得![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,从而可得平面
,从而可得平面![]() 平面
平面![]() .(2)由(1)知
.(2)由(1)知![]() 两两垂直,建立空间直角坐标系,利用平面的法向量求解即可。
两两垂直,建立空间直角坐标系,利用平面的法向量求解即可。
试题解析:
(1)证明:如图,取![]() ,
, ![]() 的中点
的中点![]() ,
, ![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
则四边形![]() 为正方形,
为正方形,
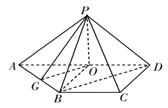
∴![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() ,
,
又![]()
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]()
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)解:由(1)知![]() 两两垂直,建立如图所示的空间直角坐标系
两两垂直,建立如图所示的空间直角坐标系![]() ,
,
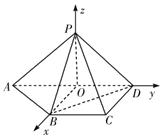
∵![]() ,
, ![]() ,
,
∴![]() .
.
令![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由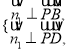 ,得
,得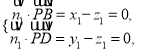 ,取
,取![]() ,得
,得![]() .
.
又设平面![]() 的法向量为
的法向量为![]() ,
,
由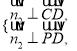 得
得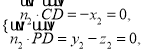 ,取
,取![]() ,得
,得![]() ,
,
∴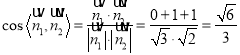 ,
,
由图形得二面角![]() 为锐角,
为锐角,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知Sn为数列{an}的前n项和,且有a1=1,Sn+1=an+1(n∈N*).
(1)求数列{an}的通项an;
(2)若bn= ![]() ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;
(3)设ck= ![]() ,{ck}的前n项和为An , 是否存在最小正整数m,使得不等式An<m对任意正整数n恒成立?若存在,求出m的值;若不存在,说明理由.
,{ck}的前n项和为An , 是否存在最小正整数m,使得不等式An<m对任意正整数n恒成立?若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市拟兴建九座高架桥,新闻媒体对此进行了问卷调查,在所有参与调查的市民中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
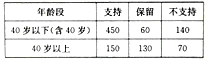
(1)在所有参与调查的人中,用分层抽样的方法抽取部分市民做进一步调研(不同态度的群体中亦按年龄分层抽样),已知从“保留”态度的人中抽取了19人,则在“支持”态度的群体中,年龄在40岁以下(含40岁)的人有多少被抽取;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在40岁以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的焦点坐标为![]() ,且短轴一顶点
,且短轴一顶点![]() 满足
满足![]() .
.
(1)求椭圆的方程;
(2)过![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时![]() 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米![]()
![]() (单位:千米/小时).假设汽油的价格是每升6元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升6元,而汽车每小时耗油![]() 升,司机的工资是每小时30元.
升,司机的工资是每小时30元.
(1)求这次行车总费用![]() 关于
关于![]() 的表达式;
的表达式;
(2)当![]() 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣ax+a+3,g(x)=ax﹣2a.
(1)若函数h(x)=f(x)﹣g(x)在[﹣2,0]上有两个零点,求实数a的取值范围;
(2)若存在x0∈R,使得f(x0)≤0与g(x0)≤0同时成立,求实数a的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com