【答案】
分析:根据题意可算出函数表达式为:f(x)=sin(2x+
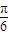
+2kπ).通过表达式计算函数值,可得①②都是真命题;根据函数图象的对称性,结合函数奇偶性的图象特征,可得③是假命题;根据正弦函数单调区间的公式,计算得f(x)的单调递增区间不是[kπ+

,kπ+
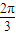
](k∈Z),得④是假命题.
解答:解:∵f(x)≤f(

)对一切x∈R恒成立,
∴f(x)=sin(2x+φ)在x=
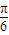
时取得最大值,即2×
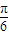
+φ=
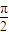
+2kπ,k∈Z,得φ=
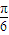
+2kπ,k∈Z,
因此函数表达式为:f(x)=sin(2x+
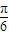
+2kπ)
因为f(-
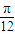
)=sin[2×(-

)+
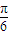
+2kπ]=sin2kπ=0,所以①是真命题;
∵f(
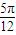
)=sin(2×
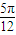
x+
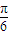
+2kπ)=sin(π+2kπ)=0,
∴x=
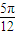
是函数y=f(x)的零点,得点(
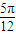
,0)是函数f(x)图象的对称中心,故②是真命题;
∵函数y=f(x)的图象既不关于y轴对称,也不关于原点对称
∴f(x)既不是奇函数也不是偶函数,得③是真命题;
令-
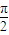
+2kπ≤2x+
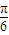
≤
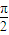
+2kπ,得-
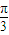
+kπ≤x≤
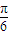
+kπ,
∴f(x)的单调递增区间是[-

+kπ,
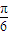
+kπ](k∈Z),故④是假命题.
由以上的讨论,可得正确命题为①②③,共三个
故答案为:①②③
点评:本题以命题真假的判断为载体,考查了三角函数的单调性、图象的对称性、函数的最值和零点等知识,属于中档题.

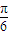 )对一切x∈R恒成立,则:
)对一切x∈R恒成立,则: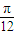 )=0;
)=0;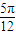 ,0)对称;
,0)对称;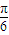 ,kπ+
,kπ+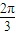 ](k∈Z)
](k∈Z)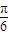 +2kπ).通过表达式计算函数值,可得①②都是真命题;根据函数图象的对称性,结合函数奇偶性的图象特征,可得③是假命题;根据正弦函数单调区间的公式,计算得f(x)的单调递增区间不是[kπ+
+2kπ).通过表达式计算函数值,可得①②都是真命题;根据函数图象的对称性,结合函数奇偶性的图象特征,可得③是假命题;根据正弦函数单调区间的公式,计算得f(x)的单调递增区间不是[kπ+ ,kπ+
,kπ+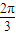 ](k∈Z),得④是假命题.
](k∈Z),得④是假命题. )对一切x∈R恒成立,
)对一切x∈R恒成立,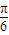 时取得最大值,即2×
时取得最大值,即2×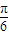 +φ=
+φ=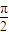 +2kπ,k∈Z,得φ=
+2kπ,k∈Z,得φ=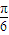 +2kπ,k∈Z,
+2kπ,k∈Z,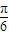 +2kπ)
+2kπ)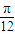 )=sin[2×(-
)=sin[2×(- )+
)+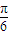 +2kπ]=sin2kπ=0,所以①是真命题;
+2kπ]=sin2kπ=0,所以①是真命题;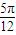 )=sin(2×
)=sin(2×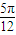 x+
x+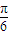 +2kπ)=sin(π+2kπ)=0,
+2kπ)=sin(π+2kπ)=0,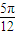 是函数y=f(x)的零点,得点(
是函数y=f(x)的零点,得点(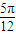 ,0)是函数f(x)图象的对称中心,故②是真命题;
,0)是函数f(x)图象的对称中心,故②是真命题;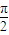 +2kπ≤2x+
+2kπ≤2x+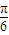 ≤
≤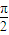 +2kπ,得-
+2kπ,得-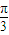 +kπ≤x≤
+kπ≤x≤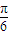 +kπ,
+kπ, +kπ,
+kπ,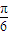 +kπ](k∈Z),故④是假命题.
+kπ](k∈Z),故④是假命题.

 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案