已知函数f(x)=x2+ax+b(a、b∈R),g(x)=2x2-4x-16,
(1)求不等式g(x)<0的解集;
(2)若|f(x)|≤|g(x)|对任意x∈R恒成立,求a,b;
(3)在(2)的条件下,若对一切x>2,均有f(x)≥(m+2)x-m-15成立,求实数m的取值范围.
【答案】
分析:(1)由g(x)=2x
2-4x-16<0,知(x+2)(x-4)<0,由此能求出不等式g(x)<0的解集.
(2)由|x
2+ax+b|≤|2x
2-4x-16|对x∈R恒成立,知当x=4,x=-2时成立,由此能求出a,b.
(3)由f(x)=x
2-2x-8,知x
2-4x+7≥m(x-1),从而得到对一切x>2,均有不等式
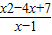
≥m成立.由此能求出实数m的取值范围.
解答:解:(1)g(x)=2x
2-4x-16<0,
∴(x+2)(x-4)<0,
∴-2<x<4.
∴不等式g(x)<0的解集为{x|-2<x<4}.…(4分)
(2)∵|x
2+ax+b|≤|2x
2-4x-16|对x∈R恒成立,
∴当x=4,x=-2时成立,
∴
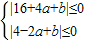
,
∴
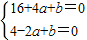
,
∴
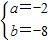
.…(8分)
(3)由(2)知,f(x)=x
2-2x-8.
∴x
2-2x-8≥(m+2)x-m-15 (x>2),
即x
2-4x+7≥m(x-1).
∴对一切x>2,均有不等式
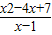
≥m成立.…(10分)
而
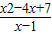
=(x-1)+
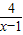
-2
≥2
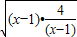
-2=2(当x=3时等号成立)
∴实数m的取值范围是(-∞,2].…(12分)
点评:本题考查不等式的解集的求法,考查满足条件的实数的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

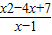 ≥m成立.由此能求出实数m的取值范围.
≥m成立.由此能求出实数m的取值范围.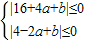 ,
,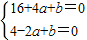 ,
,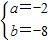 .…(8分)
.…(8分)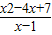 ≥m成立.…(10分)
≥m成立.…(10分)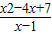 =(x-1)+
=(x-1)+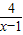 -2
-2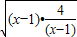 -2=2(当x=3时等号成立)
-2=2(当x=3时等号成立)

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<