
若方程 +
+ =1所表示的曲线为C,则下面四个命题
=1所表示的曲线为C,则下面四个命题
①若C为椭圆,则1<t<4 ;②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆;④若C为椭圆, 且长轴在x轴上,则1<t<
且长轴在x轴上,则1<t<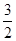
其中真命题的序号是_________.
②
【解析】
试题分析:据椭圆方程的特点列出不等式求出t的范围判断出①错,据双曲线方程的特点列出不等式求出t的范围,判断出②对;据圆方程的特点列出方程求出t的值,判断出③错;据椭圆方程的特点列出不等式求出t的范围,判断出④错.解:若C为椭圆应该满足(4-t)(t-1)>0,4-t≠t-1
即1<t<4且t≠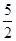 故①错,若C为双曲线应该满足(4-t)(t-1)<0即t>4或t<1故②对,当4-t=t-1即t=
故①错,若C为双曲线应该满足(4-t)(t-1)<0即t>4或t<1故②对,当4-t=t-1即t=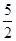 表示圆,故③错,若C表示椭圆,且长轴在x轴上应该满足4-t>t-1>0则1<t<
表示圆,故③错,若C表示椭圆,且长轴在x轴上应该满足4-t>t-1>0则1<t<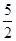 ,因此④错,故填写②
,因此④错,故填写②
考点:圆锥曲线的共同特征。
点评:主要是考查了椭圆方程于双曲线方程的标准形式的运用,属于中档题。


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
| x2 |
| 4-t |
| y2 |
| t-1 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
①若曲线C为椭圆,则2<t<4;②若曲线C为双曲线,则t>4或t<2;③曲线C不可能是圆;④若曲线C表示焦点在y轴上的椭圆,则3<t<4.
以上命题正确的是( )
A.②③ B.①④ C.②④ D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
方程![]() =1所表示的曲线为C,有下列命题:
=1所表示的曲线为C,有下列命题:
①若曲线C为椭圆,则2<t<4;②若曲线C为双曲线,则t>4或t<2;③曲线C不可能是圆;④若曲线C表示焦点在y轴上的椭圆,则3<t<4.
以上命题正确的是( )
A.②③ B.①④ C.②④ D.①②④
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省济南外国语学校高二(下)期中数学试卷(理科)(解析版) 题型:选择题
 +
+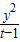 =1所表示的曲线为C,给出下列四个命题:
=1所表示的曲线为C,给出下列四个命题: .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com