
分析 由正弦定理把△ABC的边a,c用含有A的代数式表示,再由三角形为锐角三角形求出角A的范围,把$\overrightarrow{BA}•\overrightarrow{BC}$转化为关于A的三角函数求最值.
解答 解:如图,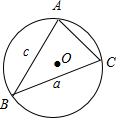
设$|\overrightarrow{BA}|=c$,$|\overrightarrow{BC}|=a$,
∵△ABC的外接圆O的半径为1,∠B=$\frac{π}{6}$,
∴$\frac{a}{sinA}=\frac{c}{sinC}=2$,则a=2sinA,c=2sinC.
C=$\frac{5π}{6}-A$,
由$\left\{\begin{array}{l}{0<A<\frac{π}{2}}\\{0<\frac{5π}{6}-A<\frac{π}{2}}\end{array}\right.$,得$\frac{π}{3}<A<\frac{π}{2}$.
∴$\overrightarrow{BA}•\overrightarrow{BC}$=ca•cos$\frac{π}{6}$=4×$\frac{\sqrt{3}}{2}$sinAsin($\frac{5π}{6}-A$)
=$2\sqrt{3}sinA(sin\frac{5π}{6}cosA-cos\frac{5π}{6}sinA)$=$\frac{\sqrt{3}}{2}sin2A+3si{n}^{2}A$
=$\frac{\sqrt{3}}{2}sin2A-\frac{3}{2}cos2A+\frac{3}{2}$=$\sqrt{3}sin(2A-\frac{π}{3})+\frac{3}{2}$.
∵$\frac{π}{3}<A<\frac{π}{2}$,∴$\frac{π}{3}<2A-\frac{π}{3}<\frac{2π}{3}$,
则$\frac{\sqrt{3}}{2}<sin(2A-\frac{π}{3})<1$.
∴$\overrightarrow{BA}•\overrightarrow{BC}$∈(3,$\frac{3}{2}+\sqrt{3}$).
故答案为:(3,$\frac{3}{2}+\sqrt{3}$).
点评 本题考查平面向量的数量积运算,考查正弦定理在解三角形中的应用,体现了数学转化思想方法,训练了三角函数最值的求法,是中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 0或$\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 感染 | 未感染 | 总计 | |
| 没服用 | 20 | 50 | |
| 服用 | 40 | ||
| 总计 | 100 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 |
| k0 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤0} | B. | {x|0≤x<1} | C. | {x|-1<x<2} | D. | {x|-1≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{10}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{4}$ | B. | $\frac{3}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在如图所示的锐角三角形空地中,有一内接矩形花园(阴影部分),其一边长为x(单位:m).将一颗豆子随机地扔到该空地内,用A表示事件:“豆子落在矩形花园内”,则P(A)的最大值为( )
在如图所示的锐角三角形空地中,有一内接矩形花园(阴影部分),其一边长为x(单位:m).将一颗豆子随机地扔到该空地内,用A表示事件:“豆子落在矩形花园内”,则P(A)的最大值为( )| A. | $\frac{1}{4}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com