解:(Ⅰ)函数的定义域为(0,+∞),
当a=3时,f′(x)=1+

-

=
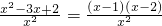
,
令f′(x)=0,解得x=1或x=2,
当0<x<1或x>2时,f′(x)>0,当1<x<2时,f′(x)<0,
所以当x=1时f(x)取得极大值f(1)=-1,当x=2时f(x)取得极小值f(2)=1-3ln2;
(Ⅱ)f′(x)=1+

-

=
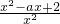
,
令g(x)=x
2-ax+2,其判别式△=a
2-8,
①当|a|

时,△≤0时,f′(x)≥0,故f(x)在(0,+∞)上单调递增;
②当a<-2

时,△>0时,g(x)=0的两根都小于0,所以在(0,+∞)上f′(x)>0,
故f(x)在(0,+∞)上单调递增;
③当a>2

时,△>0,g(x)=0的两根为:x
1=
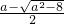
,x
2=

,且都大于0,
当0<x<x
1或x>x
2时f′(x)>0,当x
1<x<x
2时f′(x)<0,
故f(x)在(0,
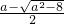
)和(

,+∞)上递增,在(
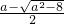
,

)上递减,
综上,当a

时f(x)(0,+∞)上单调递增;当a>

时,f(x)在(0,
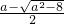
)和(

,+∞)上递增,在(
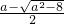
,

)上递减;
分析:(Ⅰ)先求出函数的定义域,当a=3时在定义域内解不等式f′(x)>0,f′(x)<0即可;
(Ⅱ)f′(x)=
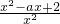
,令g(x)=x
2-ax+2,其判别式△=a
2-8,按△≤0时,△>0时两种情况解不等式f′(x)>0,f′(x)<0,△>0时再按根与0的大小讨论,即共分三种情况进行讨论解不等式即可;
点评:本题考查利用导数研究函数的极值、函数的单调性,考查分类讨论思想,考查学生分析解决问题的能力.

 -alnx(a∈R).
-alnx(a∈R). -
- =
=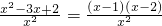 ,
, -
- =
=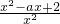 ,
, 时,△≤0时,f′(x)≥0,故f(x)在(0,+∞)上单调递增;
时,△≤0时,f′(x)≥0,故f(x)在(0,+∞)上单调递增; 时,△>0时,g(x)=0的两根都小于0,所以在(0,+∞)上f′(x)>0,
时,△>0时,g(x)=0的两根都小于0,所以在(0,+∞)上f′(x)>0, 时,△>0,g(x)=0的两根为:x1=
时,△>0,g(x)=0的两根为:x1=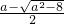 ,x2=
,x2= ,且都大于0,
,且都大于0,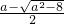 )和(
)和( ,+∞)上递增,在(
,+∞)上递增,在(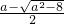 ,
, )上递减,
)上递减, 时f(x)(0,+∞)上单调递增;当a>
时f(x)(0,+∞)上单调递增;当a> 时,f(x)在(0,
时,f(x)在(0,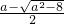 )和(
)和( ,+∞)上递增,在(
,+∞)上递增,在(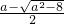 ,
, )上递减;
)上递减;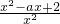 ,令g(x)=x2-ax+2,其判别式△=a2-8,按△≤0时,△>0时两种情况解不等式f′(x)>0,f′(x)<0,△>0时再按根与0的大小讨论,即共分三种情况进行讨论解不等式即可;
,令g(x)=x2-ax+2,其判别式△=a2-8,按△≤0时,△>0时两种情况解不等式f′(x)>0,f′(x)<0,△>0时再按根与0的大小讨论,即共分三种情况进行讨论解不等式即可;
