
【题目】如图,已知抛物线y2=4x,过点P(2,0)作斜率分别为k1 , k2的两条直线,与抛物线相交于点A、B和C、D,且M、N分别是AB、CD的中点 
(1)若k1+k2=0, ![]() ,求线段MN的长;
,求线段MN的长;
(2)若k1k2=﹣1,求△PMN面积的最小值.
【答案】
(1)解:设A(x1,y1),B(x2,y2),不妨设y1>0,则
设直线AB的方程为y=k1(x﹣2),代入y2=4x,可得y2﹣ ![]() y﹣8=0
y﹣8=0
∴y1+y2= ![]() ,y1y2=﹣8,
,y1y2=﹣8,
∵ ![]() ,∴y1=﹣2y2,∴y1=4,y2=﹣2,
,∴y1=﹣2y2,∴y1=4,y2=﹣2,
∴yM=1,
∵k1+k2=0,
∴线段AB和CD关于x轴对称,
∴线段MN的长为2
(2)解:∵k1k2=﹣1,∴两直线互相垂直,
设AB:x=my+2,则CD:x=﹣ ![]() y+2,
y+2,
x=my+2代入y2=4x,得y2﹣4my﹣8=0,
则y1+y2=4m,y1y2=﹣8,
∴M(2m2+2,2m).
同理N( ![]() +2,﹣
+2,﹣ ![]() ),
),
∴|PM|=2|m| ![]() ,|PN|=
,|PN|= ![]()
![]() ,|
,|
∴S△PMN= ![]() |PM||PN|=
|PM||PN|= ![]() (m2+1)=2(|m|+
(m2+1)=2(|m|+ ![]() )≥4,
)≥4,
当且仅当m=±1时取等号,
∴△PMN面积的最小值为4
【解析】(1)若k1+k2=0,线段AB和CD关于x轴对称,利用 ![]() ,确定坐标之间的关系,即可求线段MN的长;(2)若k1k2=﹣1,两直线互相垂直,求出M,N的坐标,可得|PM|,|PN|,即可求△PMN面积的最小值.
,确定坐标之间的关系,即可求线段MN的长;(2)若k1k2=﹣1,两直线互相垂直,求出M,N的坐标,可得|PM|,|PN|,即可求△PMN面积的最小值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(2)现往袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和不大于4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为
为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为![]() .设点
.设点![]() ,连接PA交椭圆于点C,坐标原点为O.
,连接PA交椭圆于点C,坐标原点为O.
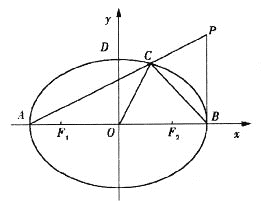
(I)求椭圆E的方程;
(II)若三角形ABC的面积不大于四边形OBPC的面积,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且an是Sn与2的等差中项,数列{bn}中,b1=1,点P(bn , bn+1)在直线x﹣y+2=0上.
(1)求a1和a2的值;
(2)求数列{an},{bn}的通项an和bn;
(3)设cn=anbn , 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;
(Ⅱ)若c= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出定义:若m﹣ ![]() <x≤m+
<x≤m+ ![]() (其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m,设函数f(x)=x﹣{x},二次函数g(x)=ax2+bx,若函数y=f(x)与y=g(x)的图象有且只有一个公共点,则a,b的取值不可能是( )
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m,设函数f(x)=x﹣{x},二次函数g(x)=ax2+bx,若函数y=f(x)与y=g(x)的图象有且只有一个公共点,则a,b的取值不可能是( )
A.a=﹣4,b=1
B.a=﹣2,b=﹣1
C.a=4,b=﹣1
D.a=5,b=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且 ![]() bcosA=asinB.
bcosA=asinB.
(1)求角A的大小;
(2)若a=6,△ABC的面积是9 ![]() ,求三角形边b,c的长.
,求三角形边b,c的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com