
已知函数 .
.
(1) 当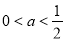 时,讨论
时,讨论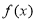 的单调性;
的单调性;
(2)设 ,当
,当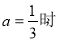 若对任意
若对任意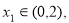 存在
存在 使
使 求实数
求实数 的取值范围。
的取值范围。
(1)f(x)在(0,1),(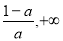 )上是增函数,在(1,
)上是增函数,在(1,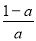 )上是减函数;(2)
)上是减函数;(2)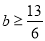 .
.
【解析】
试题分析:(1)根据题意可以求得 ,当
,当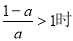 ,即
,即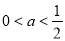 时,可通过列表通过f’(x)的正负性来判断f(x)的单调性;
时,可通过列表通过f’(x)的正负性来判断f(x)的单调性;
可将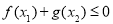 变形为
变形为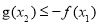 ,∴问题就等价于求当
,∴问题就等价于求当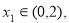 存在
存在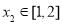 ,使
,使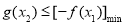 成立的b的取值范围,而
成立的b的取值范围,而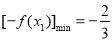 ,∴问题进一步等价于求存在
,∴问题进一步等价于求存在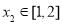 ,使
,使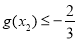 时b的取值范围,通过参变分离,可得存在
时b的取值范围,通过参变分离,可得存在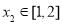 ,求使2b≥
,求使2b≥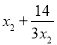 成立b的范围,∴只需2b≥
成立b的范围,∴只需2b≥ 即可.
即可.
(1) 3分
3分
当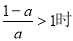 ,即
,即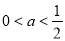 时,此时f(x)的单调性如下:
时,此时f(x)的单调性如下:
x | (0,1) | 1 | (1, |
| ( |
| + | 0 | - | 0 | + |
f(x) | 增 |
| 减 |
| 增 |
当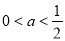 时,f(x)在(0,1),(
时,f(x)在(0,1),(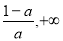 )上是增函数,在(1,
)上是增函数,在(1,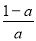 )上是减函数 7分;
)上是减函数 7分;
(2)由(1)知,当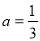 时,f(x)在(0,1)上是增函数,在(1,2)上是减函数.
时,f(x)在(0,1)上是增函数,在(1,2)上是减函数.
于是
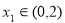 时,
时, 8分
8分
从而存在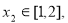 使
使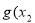 )=
)=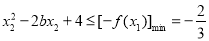 10分
10分
变形可得存在存在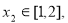 使2b≥
使2b≥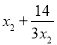 成立 11分
成立 11分
∴只需2b≥ 成立 12分
成立 12分
显然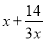 在(1,2)上单调递减,∴只需2b≥
在(1,2)上单调递减,∴只需2b≥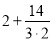 ,即
,即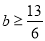 14分
14分
考点:1、利用导数讨论函数的单调性;2、利用导数求函数的最值解决恒成立问题与存在性问题.


科目:高中数学 来源:2015届湖南省益阳市高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
已知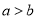 ,椭圆
,椭圆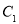 的方程为
的方程为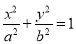 ,双曲线
,双曲线 的方程为
的方程为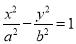 ,
, 与
与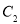 的离心率之积为
的离心率之积为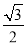 ,则
,则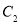 的渐近线方程为( )
的渐近线方程为( )
A.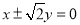 B.
B.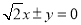 C.
C.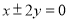 D.
D.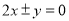
查看答案和解析>>
科目:高中数学 来源:2015届湖北省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知命题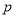 :
: ,命题
,命题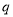 :
: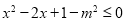 (
(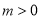 ).
).
若“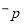 ”是“
”是“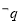 ”的必要而不充分条件,求实数
”的必要而不充分条件,求实数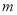 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届湖北省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
椭圆
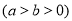 的一个焦点为
的一个焦点为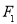 ,若椭圆上存在一个点
,若椭圆上存在一个点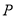 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段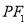 相切于该线段的中点,则椭圆的离心率为( )
相切于该线段的中点,则椭圆的离心率为( )
A. B.
B.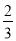 C.
C.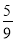 D.
D.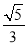
查看答案和解析>>
科目:高中数学 来源:2015届湖北省襄阳市四校高二下学期期中联考文科数学试卷(解析版) 题型:填空题
过双曲线C:
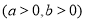 的一个焦点作圆
的一个焦点作圆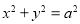 的两条切线,切点分别为
的两条切线,切点分别为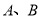 ,若
,若 (
(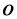 是坐标原点),则双曲线C的离心率为____;
是坐标原点),则双曲线C的离心率为____;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com