
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
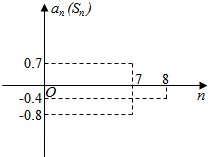 已知等差数列{an}的前n项和为Sn,在同一坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示.
已知等差数列{an}的前n项和为Sn,在同一坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
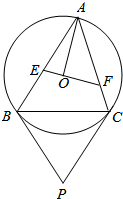 如图,锐角△ABC内接于圆0.过圆心0且垂直于半径0A的直线分别交边AB、AC于点E、F.设圆0在B、C两点处的切线相交于点P.求证:直线AP平分线段EF.
如图,锐角△ABC内接于圆0.过圆心0且垂直于半径0A的直线分别交边AB、AC于点E、F.设圆0在B、C两点处的切线相交于点P.求证:直线AP平分线段EF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 装潢师小王在墙面上设计了如图所示的一个图案,已知四边形四个顶点都在圆周上,且AD=DC=4m,BC=6m,∠A=120°,现在小王想买乳胶漆给四边形ABCD涂色,依据设计方案四边形的四边涂成红色,四边形内部要涂成蓝色,他想根据线段的长度与四边形的面积来买乳胶漆.请你帮他计算:
装潢师小王在墙面上设计了如图所示的一个图案,已知四边形四个顶点都在圆周上,且AD=DC=4m,BC=6m,∠A=120°,现在小王想买乳胶漆给四边形ABCD涂色,依据设计方案四边形的四边涂成红色,四边形内部要涂成蓝色,他想根据线段的长度与四边形的面积来买乳胶漆.请你帮他计算:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com