
正方体ABCD-A1B1C1D1中,E,F分别是线段C1D,BC的中点,则直线A1B与直线EF的位置关系是( )
(A)相交 (B)异面 (C)平行 (D)垂直
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(九)第二章第六节练习卷(解析版) 题型:选择题
对于任意a∈[-1,1],函数f(x)=x2+(a-4)x+4-2a的值恒大于零,那么x的取值范围是( )
(A)(1,3) (B)(-∞,1)∪(3,+∞)
(C)(1,2) (D)(3,+∞)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(一)第一章第一节练习卷(解析版) 题型:填空题
设S为复数集C的非空子集.若对任意x,y∈S,都有x+y,x-y,xy∈S,则称S为封闭集.下列命题:
①集合S={a+bi|a,b为整数,i为虚数单位}为封闭集;
②若S为封闭集,则一定有0∈S;
③封闭集一定是无限集;
④若S为封闭集,则满足S⊆T⊆C的任意集合T也是封闭集.
其中真命题有 (写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十四第七章第三节练习卷(解析版) 题型:解答题
直三棱柱ABC-A1B1C1的底面为等腰直角三角形,∠BAC=90°,AB=AC=2,AA1=2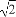 ,E,F分别是BC,AA1的中点.
,E,F分别是BC,AA1的中点.
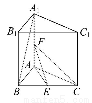
求(1)异面直线EF和A1B所成的角.
(2)三棱锥A-EFC的体积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十四第七章第三节练习卷(解析版) 题型:选择题
设P表示一个点,a,b表示两条直线,α,β表示两个平面,给出下列命题,其中正确的命题是( )
①P∈a,P∈α⇒a?α;
②a∩b=P,b?β⇒a?β;
③a∥b,a?α,P∈b,P∈α⇒b?α;
④α∩β=b,P∈α,P∈β⇒P∈b.
(A)①② (B)②③ (C)①④ (D)③④
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷(解析版) 题型:解答题
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC,点E是棱PB上的动点.
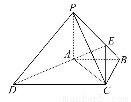
(1)若PD∥平面EAC,试确定点E在棱PB上的位置.
(2)在(1)的条件下,求二面角A-CE-P的余弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷(解析版) 题型:选择题
已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题,如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题有( )
(A)0个 (B)1个 (C)2个 (D)3个
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷(解析版) 题型:选择题
设平面α的法向量为(1,2,-2),平面β的法向量为(-2,-4,k),若α∥β,则k等于( )
(A)2 (B)-4 (C)4 (D)-2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十九第七章第八节练习卷(解析版) 题型:选择题
在正方体ABCD-A1B1C1D1中,二面角A1-BD-C1的余弦值为( )
(A)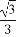 (B)
(B)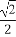 (C)
(C) (D)
(D)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com