
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:选择题
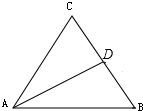 如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )
如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )| A. | $\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{AD}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AB}$+$\overrightarrow{DC}$=$\overrightarrow{AD}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{DC}$=$\overrightarrow{BC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
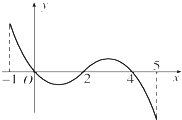 已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨(¬q) | B. | p∧(¬q) | C. | p∨q | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
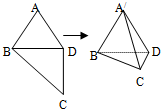 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(4).
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(4).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{{\begin{array}{l}{x=sinφ}\\{y={{cos}^2}φ}\end{array}}\right.$(φ为参数) | B. | $\left\{\begin{array}{l}{x=cosφ}\\{y=si{n}^{2}φ}\end{array}\right.$(φ为参数) | ||
| C. | $\left\{\begin{array}{l}{x=\sqrt{1-r}}\\{y=r}\end{array}\right.$(r为参数) | D. | $\left\{\begin{array}{l}{x=tanφ}\\{y=1-ta{n}^{2}φ}\end{array}\right.$(φ为参数) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com