
【题目】在正方体ABCD﹣A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值t构成的集合是( ) 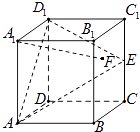
A.{t| ![]() }
}
B.{t| ![]() ≤t≤2}
≤t≤2}
C.{t|2 ![]() }
}
D.{t|2 ![]() }
}
【答案】D
【解析】解:设平面AD1E与直线BC交于点G,连接AG、EG,则G为BC的中点 分别取B1B、B1C1的中点M、N,连接AM、MN、AN,则
∵A1M∥D1E,A1M平面D1AE,D1E平面D1AE,
∴A1M∥平面D1AE.同理可得MN∥平面D1AE,
∵A1M、MN是平面A1MN内的相交直线
∴平面A1MN∥平面D1AE,
由此结合A1F∥平面D1AE,可得直线A1F平面A1MN,即点F是线段MN上上的动点.
设直线A1F与平面BCC1B1所成角为θ
运动点F并加以观察,可得
当F与M(或N)重合时,A1F与平面BCC1B1所成角等于∠A1MB1 , 此时所成角θ达到最小值,满足tanθ= ![]() =2;
=2;
当F与MN中点重合时,A1F与平面BCC1B1所成角达到最大值,满足tanθ= ![]() =2
=2 ![]()
∴A1F与平面BCC1B1所成角的正切取值范围为[2,2 ![]() ]
]
故选:D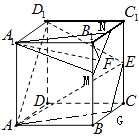
设平面AD1E与直线BC交于点G,连接AG、EG,则G为BC的中点.分别取B1B、B1C1的中点M、N,连接AM、MN、AN,可证出平面A1MN∥平面D1AE,从而得到A1F是平面A1MN内的直线.由此将点F在线段MN上运动并加以观察,即可得到A1F与平面BCC1B1所成角取最大值、最小值的位置,由此不难得到A1F与平面BCC1B1所成角的正切取值范围.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,其公差为﹣2,且a7是a3与a9的等比中项,Sn为{an}的前n项和,n∈N* , 则S10的值为( )
A.﹣110
B.﹣90
C.90
D.110
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() .过原点
.过原点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上的点,若
上的点,若![]() ,
, ![]() ,且
,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2) 设椭圆在点![]() 处的切线记为直线
处的切线记为直线![]() ,点
,点![]() 在
在![]() 上的射影分别为
上的射影分别为![]() ,过
,过![]() 作
作![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,试问
,试问![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种仪器的元件,由于受生产能力和技术水平等因素的限制,会产生一些次品,根据经验知道,次品数P(万件)与日产量x(万件)之间满足关系: 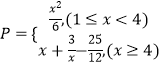 已知每生产l万件合格的元件可以盈利2万元,但每生产l万件次品将亏损1万元.(利润=盈利一亏损)
已知每生产l万件合格的元件可以盈利2万元,但每生产l万件次品将亏损1万元.(利润=盈利一亏损)
(1)试将该工厂每天生产这种元件所获得的利润T(万元)表示为日产量x(万件)的函数;
(2)当工厂将这种仪器的元件的日产量x定为多少时获得的利润最大,最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax2﹣bx﹣1,其中a,b∈R,e=2.71828…为自然对数的底数.
(1)设g(x)是函数f(x)的导函数,求函数g(x)在区间[0,1]上的最小值;
(2)若f(1)=0,函数f(x)在区间(0,1)内有零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆x2+y2=1上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(1)写出C的参数方程;
(2)设直线l:2x+y﹣2=0与C的交点为P1 , P2 , 以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1P2的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式组 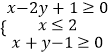 表示的平面区域为D,则
表示的平面区域为D,则
(1)z=x2+y2的最小值为 .
(2)若函数y=|2x﹣1|+m的图象上存在区域D上的点,则实数m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
顾客数(人) | x | 30 | 25 | y | 10 |
结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
已知这100位顾客中一次购物量超过8件的顾客占55%.
(Ⅰ)确定x,y的值,并求顾客一次购物的结算时间X的分布列与数学期望;
(Ⅱ)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2.5分钟的概率.
(注:将频率视为概率)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com