
【题目】某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
顾客数(人) | x | 30 | 25 | y | 10 |
结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
已知这100位顾客中一次购物量超过8件的顾客占55%.
(Ⅰ)确定x,y的值,并求顾客一次购物的结算时间X的分布列与数学期望;
(Ⅱ)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2.5分钟的概率.
(注:将频率视为概率)
【答案】(Ⅰ)x=15,y=20.
X | 1 | 1.5 | 2 | 2.5 | 3 |
P |
|
|
|
|
|
E(X)=1.9;(Ⅱ) ![]()
【解析】试题分析:(Ⅰ)根据总人数有100人,则![]() ,由100位顾客中一次购物量超过8件的顾客占55%,则知
,由100位顾客中一次购物量超过8件的顾客占55%,则知![]() .根据这两式得x=15,y=20,由表格可得X的可以取值为:1,1.5,2,2.5,3;该超市所有顾客一次购物的结算时间组成一个总体,所收集的100位顾客一次购物的结算时间可视为总体的一个容量为100的简单随机样本,将频率视为概率,即可得到分布列与期望.
.根据这两式得x=15,y=20,由表格可得X的可以取值为:1,1.5,2,2.5,3;该超市所有顾客一次购物的结算时间组成一个总体,所收集的100位顾客一次购物的结算时间可视为总体的一个容量为100的简单随机样本,将频率视为概率,即可得到分布列与期望.
(Ⅱ)由于该客到达收银台时前面恰有2位顾客需结算,则该顾客结算前的等候时间不超过2.5分钟的情况为(1、1),(1、1.5),(1.5、1)三种情况,则按照各顾客的结算相互独立,有
P(A)=P(X1=1)×P(X2=1)+P(X1=1)×P(X2=1.5)+P(X1=1.5)×P(X2=1)
=![]() ×
×![]() +
+![]() ×
×![]() +
+![]() ×
×![]() =
=![]() .
.
试题解析:(Ⅰ)由已知,得25+y+10=55,x+30=45,所以x=15,y=20.
该超市所有顾客一次购物的结算时间组成一个总体,所收集的100位顾客一次购物的结算时间可视为总体的一个容量为100的简单随机样本,将频率视为概率得
P(X=1)=![]() =
=![]() ,P(X=1.5)=
,P(X=1.5)=![]() =
=![]() ,P(X=2)=
,P(X=2)=![]() =
=![]() ,
,
P(X=2.5)=![]() =
=![]() ,P(X=3)=
,P(X=3)=![]() =
=![]() .
.
X的分布列为
X | 1 | 1.5 | 2 | 2.5 | 3 |
P |
|
|
|
|
|
X的数学期望为
E(X)=1×+1.5×![]() +2×
+2×![]() +2.5×
+2.5×![]() +3×
+3×![]() =1.9.
=1.9.
(Ⅱ)记A为事件“该顾客结算前的等候时间不超过2.5分钟”,Xi(i=1,2)为该顾客前面第i位顾客的结算时间,则
P(A)=P(X1=1且X2=1)+P(X1=1且X2=1.5)+P(X1=1.5且X2=1).
由于各顾客的结算相互独立,且X1,X2的分布列都与X的分布列相同,所以
P(A)=P(X1=1)×P(X2=1)+P(X1=1)×P(X2=1.5)+P(X1=1.5)×P(X2=1)
=![]() ×
×![]() +
+![]() ×
×![]() +
+![]() ×
×![]() =
=![]() .
.
故该顾客结算前的等候时间不超过2.5分钟的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知直线l:ax﹣y+1=0与x轴,y轴分别交于点A,B.
(1)若a>0,点M(1,﹣1),点N(1,4),且以MN为直径的圆过点A,求以AN为直径的圆的方程;
(2)以线段AB为边在第一象限作等边三角形ABC,若a=﹣ ![]() ,且点P(m,
,且点P(m, ![]() )(m>0)满足△ABC与△ABP的面积相等,求m的值.
)(m>0)满足△ABC与△ABP的面积相等,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值t构成的集合是( ) 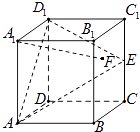
A.{t| ![]() }
}
B.{t| ![]() ≤t≤2}
≤t≤2}
C.{t|2 ![]() }
}
D.{t|2 ![]() }
}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(4,﹣3),B(2,﹣1)和直线l:4x+3y﹣2=0.
(1)求在直角坐标平面内满足|PA|=|PB|的点P的方程;
(2)求在直角坐标平面内一点P满足|PA|=|PB|且点P到直线l的距离为2的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2x+2 ![]() sinxcosx﹣sin2x.
sinxcosx﹣sin2x.
(1)求f(x)的最小正周期和值域;
(2)在△ABC中,角A,B,C所对的边分别是a,b,c,若 ![]() 且a2=bc,试判断△ABC的形状.
且a2=bc,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)两相邻的零点之间的距离为 ![]() ,将f(x)的图象向左平移
,将f(x)的图象向左平移 ![]() 个单位后图象对应的函数g(x)是偶函数. (Ⅰ)求函数f(x)的解析式;
个单位后图象对应的函数g(x)是偶函数. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)的对称轴及单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设离心率为 ![]() 的椭圆
的椭圆![]() 的左、右焦点为
的左、右焦点为![]() , 点P是E上一点,
, 点P是E上一点, ![]() ,
, ![]() 内切圆的半径为
内切圆的半径为 ![]() .
.
(1)求E的方程;
(2)矩形ABCD的两顶点C、D在直线![]() 上,A、B在椭圆E上,若矩形ABCD的周长为
上,A、B在椭圆E上,若矩形ABCD的周长为 ![]() , 求直线AB的方程.
, 求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图并判断是否线性相关;
(2)如果线性相关,求线性回归方程;
(3)估计使用年限为10年时,维修费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
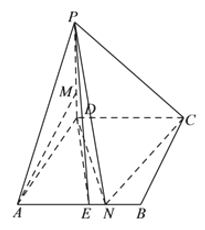
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 中点.
中点.
(I)求证:直线![]() 平面
平面![]() .
.
(II)求证:直线![]() 平面
平面![]() .
.
(III)在![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,若存在,确定
,若存在,确定![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com