
【题目】已知直线l:ax﹣y+1=0与x轴,y轴分别交于点A,B.
(1)若a>0,点M(1,﹣1),点N(1,4),且以MN为直径的圆过点A,求以AN为直径的圆的方程;
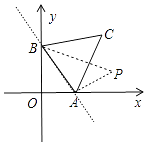
(2)以线段AB为边在第一象限作等边三角形ABC,若a=﹣ ![]() ,且点P(m,
,且点P(m, ![]() )(m>0)满足△ABC与△ABP的面积相等,求m的值.
)(m>0)满足△ABC与△ABP的面积相等,求m的值.
【答案】
(1)解:由题意A(﹣ ![]() ,0),AM⊥AN,
,0),AM⊥AN,
∴ ![]() =﹣1,∵a>0,∴a=1,
=﹣1,∵a>0,∴a=1,
∴A(﹣1,0),∵N(1,4),
∴AN的中点坐标为D(0,2),|AD|= ![]() ,
,
∴以AN为直径的圆的方程是x2+(y﹣2)2=5;
(2)解:根据题意画出图形,如图所示:
由直线y=﹣ ![]() x+1,令x=0,解得y=1,
x+1,令x=0,解得y=1,
故点B(0,1),
令y=0,解得x= ![]() ,故点A(
,故点A( ![]() ,0),
,0),
∵△ABC为等边三角形,且OA= ![]() ,OB=1,
,OB=1,
根据勾股定理得:AB=2,即等边三角形的边长为2,
故过C作AB边上的高为 ![]() ,即点C到直线AB的距离为
,即点C到直线AB的距离为 ![]() ,
,
由题意△ABP和△ABC的面积相等,
则P到直线AB的距离d= ![]() |﹣
|﹣ ![]() m+
m+ ![]() |=
|= ![]() ,
,
∵m>0,
∴m= ![]() .
.
【解析】(1)求出A的坐标,即可求以AN为直径的圆的方程;(2)根据题意画出图形,令直线方程中x与y分别为0,求出相应的y与x的值,确定出点A与B的坐标,进而求出AB的长即为等边三角形的边长,求出等边三角形的高即为点C到直线AB的距离,由△ABP和△ABC的面积相等,得到点C与点P到直线AB的距离相等,利用点到直线的距离公式表示出点P到直线AB的距离d,让d等于求出的高列出关于m的方程,求出方程的解即可得到m的值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,其公差为﹣2,且a7是a3与a9的等比中项,Sn为{an}的前n项和,n∈N* , 则S10的值为( )
A.﹣110
B.﹣90
C.90
D.110
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是偶函数.
是偶函数.
(1)求![]() 的值;
的值;
(2)若函数![]() 的图像与直线
的图像与直线![]() 没有交点,求
没有交点,求![]() 的取值范围;
的取值范围;
(3)若函数![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 最小值为0,若存在,求出
最小值为0,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)利用“五点法”画出函数 ![]() 在
在 ![]() 内的简图
内的简图
x | |||||
| |||||
y |

(2)若对任意x∈[0,2π],都有f(x)﹣3<m<f(x)+3恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1的各个顶点与各棱的中点共20个点中,任取2点连成直线,在这些直线中任取一条,它与对角线BD1垂直的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() .过原点
.过原点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上的点,若
上的点,若![]() ,
, ![]() ,且
,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2) 设椭圆在点![]() 处的切线记为直线
处的切线记为直线![]() ,点
,点![]() 在
在![]() 上的射影分别为
上的射影分别为![]() ,过
,过![]() 作
作![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,试问
,试问![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种仪器的元件,由于受生产能力和技术水平等因素的限制,会产生一些次品,根据经验知道,次品数P(万件)与日产量x(万件)之间满足关系: 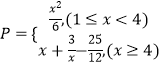 已知每生产l万件合格的元件可以盈利2万元,但每生产l万件次品将亏损1万元.(利润=盈利一亏损)
已知每生产l万件合格的元件可以盈利2万元,但每生产l万件次品将亏损1万元.(利润=盈利一亏损)
(1)试将该工厂每天生产这种元件所获得的利润T(万元)表示为日产量x(万件)的函数;
(2)当工厂将这种仪器的元件的日产量x定为多少时获得的利润最大,最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
顾客数(人) | x | 30 | 25 | y | 10 |
结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
已知这100位顾客中一次购物量超过8件的顾客占55%.
(Ⅰ)确定x,y的值,并求顾客一次购物的结算时间X的分布列与数学期望;
(Ⅱ)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2.5分钟的概率.
(注:将频率视为概率)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com