
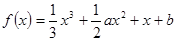
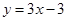 , 求
, 求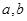 的值;
的值;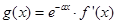 , 求函数
, 求函数 的单调区间.
的单调区间. 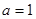 ,
,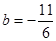 .
.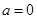 时,
时, 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 ;
;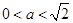 时,
时, 的单调递增区间为
的单调递增区间为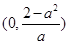 ,单调递减区间为
,单调递减区间为 和
和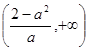 ,
,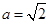 时,
时, 的单调递减区间为
的单调递减区间为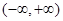 ;
; 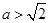 时,
时, 的单调递增区间为
的单调递增区间为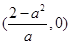 ,单调递减区间为
,单调递减区间为 ,
,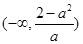 .
. 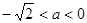 时,
时, 的单调递减区间为
的单调递减区间为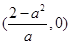 ,单调递增区间为
,单调递增区间为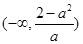 和
和 ,
,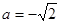 时,
时, 的单调递增区间为
的单调递增区间为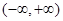 ;
; 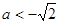 时,
时, 的单调递增区间为
的单调递增区间为 和
和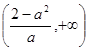 ,单调递减区间为
,单调递减区间为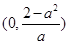 .
. 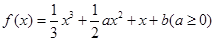 ,∴
,∴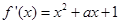
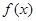 在
在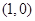 处切线方程为
处切线方程为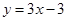 ,
, ∴
∴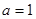 ,
,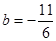 ,求解得到。
,求解得到。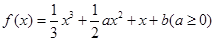 ,
,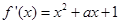 . ……1分
. ……1分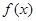 在
在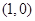 处切线方程为
处切线方程为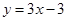 ,
, , ……3分
, ……3分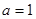 ,
,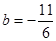 . (各1分) ……5分
. (各1分) ……5分
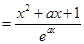
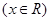 .
.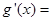
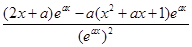
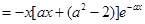 . ……7分
. ……7分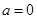 时,
时,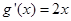 ,
, 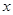 |  | 0 |  |
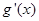 | - | 0 | + |
 |  | 极小值 |  |
 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 . …9分
. …9分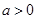 时,令
时,令 ,得
,得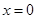 或
或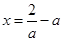 ……10分
……10分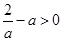 ,即
,即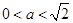 时,
时,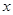 |  | 0 | 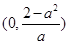 | 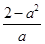 | 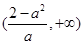 |
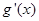 | - | 0 | + | 0 | - |
 |  | 极小值 |  | 极大值 |  |
 的单调递增区间为
的单调递增区间为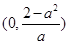 ,单调递减区间为
,单调递减区间为 ,
,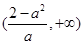 ;---11分
;---11分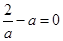 ,即
,即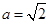 时,
时,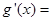
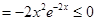 ,
, 在
在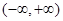 单调递减; ……12分
单调递减; ……12分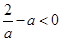 ,即
,即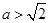 时,
时,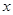 | 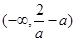 | 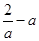 | 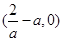 | 0 |  |
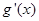 | - | 0 | + | 0 | - |
 |  | 极小值 |  | 极大值 |  |
 在
在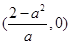 上单调递增,在
上单调递增,在 ,
,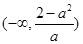 上单调递 …13分
上单调递 …13分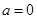 时,
时, 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 ;
;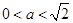 时,
时, 的单调递增区间为
的单调递增区间为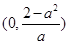 ,单调递减区间为
,单调递减区间为 和
和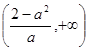 ,
,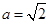 时,
时, 的单调递减区间为
的单调递减区间为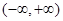 ;
; 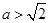 时,
时, 的单调递增区间为
的单调递增区间为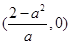 ,单调递减区间为
,单调递减区间为 ,
,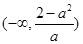 .
. 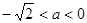 时,
时, 的单调递减区间为
的单调递减区间为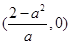 ,单调递增区间为
,单调递增区间为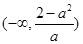 和
和 ,
,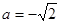 时,
时, 的单调递增区间为
的单调递增区间为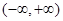 ;
; 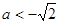 时,
时, 的单调递增区间为
的单调递增区间为 和
和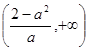 ,单调递减区间为
,单调递减区间为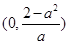


科目:高中数学 来源:不详 题型:解答题
 与时刻
与时刻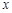 (时) 的关系为
(时) 的关系为 ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且 .
. ,
,  ,写出该函数的单调区间,并选择其中一种情形进行证明;
,写出该函数的单调区间,并选择其中一种情形进行证明;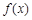 的最大值作为当天的综合放射性污染指数,并记作
的最大值作为当天的综合放射性污染指数,并记作 ,求
,求 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,
,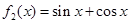 ,
,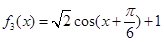 ,
,A.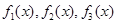 两两为“同形”函数 两两为“同形”函数 |
B.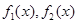 为“同形”函数,且它们与 为“同形”函数,且它们与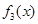 不为“同形”函数 不为“同形”函数 |
C.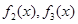 为“同形”函数,且它们与 为“同形”函数,且它们与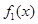 不为“同形”函数 不为“同形”函数 |
D.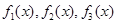 两两不为“同形”函数 两两不为“同形”函数 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
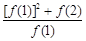 +
+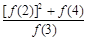 +
+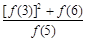 +
+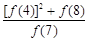 +
+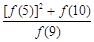 的值为_______________.
的值为_______________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com