
正实数数列{an}中,a1=1,a2=5,且{ }成等差数列.
}成等差数列.
(1)证明:数列{an}中有无穷多项为无理数;
(2)当n为何值时,an为整数?并求出使an<200的所有整数项的和.
(1)证明:由已知有: =1+24(n-1),
=1+24(n-1),
从而an=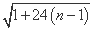 .
.
取n-1=242k-1,则an=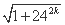 (k∈N*).
(k∈N*).
用反证法证明这些an都是无理数.
假设an=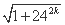 为有理数,则an必为正整数,
为有理数,则an必为正整数,
且an>24k,故an-24k≥1,an+24k>1,与(an-24k)(an+24k)=1矛盾,
所以an=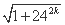 (k∈N*)都是无理数,
(k∈N*)都是无理数,
即数列{an}中有无穷多项为无理数.
(2)解:要使an为整数,由(an-1)(an+1)=24(n-1)可知:an-1,an+1同为偶数,且其中一个必为3的倍数,
所以有an-1=6m或an+1=6m.
当an=6m+1时,有 =36m2+12m+1=1+12m(3m+1)(m∈N).
=36m2+12m+1=1+12m(3m+1)(m∈N).
又m(3m+1)必为偶数,
所以an=6m+1(m∈N)满足 =1+24(n-1),
=1+24(n-1),
即n=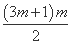 +1(m∈N)时,an为整数;
+1(m∈N)时,an为整数;
同理an=6m-1(m∈N*)时,有 =36m2-12m+1=1+12m(3m-1)(m∈N*)也满足
=36m2-12m+1=1+12m(3m-1)(m∈N*)也满足 =1+24(n-1),
=1+24(n-1),
即n=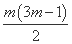 +1(m∈N*)时,an为整数;
+1(m∈N*)时,an为整数;
显然an=6m-1(m∈N*)和an=6m+1(m∈N)是数列中的不同项,
所以当n=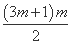 +1(m∈N)和n=
+1(m∈N)和n=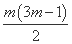 +1(m∈N*)时,an为整数.
+1(m∈N*)时,an为整数.
由an=6m+1<200(m∈N)有0≤m≤33,
由an=6m-1<200(m∈N*)有1≤m≤33.
设an中满足an<200的所有整数项的和为S,
则S=(1+7+13+…+199)+(5+11+…+197)=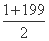 ×34+
×34+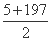 ×33=6733.
×33=6733.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
已知抛物线C:y2=8x与点M(-2,2),过C的焦点且斜率为k的直线与C交于A、B两点,若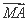 ·
·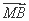 =0,则k等于( )
=0,则k等于( )
(A)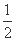 (B)
(B)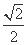 (C)
(C)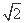 (D)2
(D)2
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆O的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段AE的长为 .

查看答案和解析>>
科目:高中数学 来源: 题型:
如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,那么( )
(A)△A1B1C1和△A2B2C2都是锐角三角形
(B)△A1B1C1和△A2B2C2都是钝角三角形
(C)△A1B1C1是钝角三角形,△A2B2C2是锐角三角形
(D)△A1B1C1是锐角三角形,△A2B2C2是钝角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
函数f(x)=sin 2x+2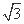 cos2x-
cos2x-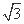 ,函数g(x)=
,函数g(x)=
mcos(2x-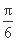 )-2m+3(m>0),若存在x1,x2∈[0,
)-2m+3(m>0),若存在x1,x2∈[0,  ],使得f(x1)=g(x2)成立,则实数m的取值范围是 .
],使得f(x1)=g(x2)成立,则实数m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
设双曲线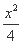 -
-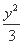 =1的左、右焦点分别为F1,F2,过F1的直线l交双曲线左支于A、B两点,则|BF2|+|AF2|的最小值为( )
=1的左、右焦点分别为F1,F2,过F1的直线l交双曲线左支于A、B两点,则|BF2|+|AF2|的最小值为( )
(A)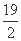 (B)11 (C)12 (D)16
(B)11 (C)12 (D)16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com