练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆O的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段AE的长为　　　　. 


    4

    解析:如图所示,连接OE,OC.

    ∵直线l与圆O相切于点C,

    ∴OC⊥l.

    又∵AD⊥l,

    ∴OC∥AD,

    ∴∠DAB=∠COB.

    又圆O的直径AB=8,BC=4,

    ∴△COB为等边三角形,

    ∴∠COB=60°,∴∠DAB=60°,

    ∴△AEO也为等边三角形,

    ∴AE=OA=4.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是(　　)

    (A)(0,2)         (B)[0,2]

    (C)(2,+∞)  (D)[2,+∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    “x>0”是“x+≥2”的(　　)

    (A)充分但不必要条件

    (B)必要但不充分条件

    (C)充分且必要条件

    (D)既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,已知Rt△ABC的两条直角边AC,BC的长分别为3 cm,4 cm,以AC为直径的圆与AB交于点D,则BD=　　　　 cm. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示,AB是☉O的直径,弦BD、CA的延长线相交于点E,F为BA延长线上一点,且BD·BE=BA·BF,求证:

    (1)EF⊥FB;

    (2)∠DFB+∠DBC=90°.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    正实数数列{an}中,a1=1,a2=5,且{}成等差数列.

    (1)证明:数列{an}中有无穷多项为无理数;

    (2)当n为何值时,an为整数?并求出使an<200的所有整数项的和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a,b,c,d∈(0,+∞),若a+d=b+c且|a-d|<|b-c|,则有(　　)

    (A)ad=bc    (B)ad<bc

    (C)ad>bc    (D)ad≤bc

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)= 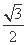-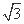sin2ωx-sin ωxcos ωx(ω>0),且y=f(x)图象的一个对称中心到最近的对称轴的距离为.

    (1)求ω的值;

    (2)求f(x)在区间[π, 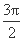]上的最大值和最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知双曲线-=1的离心率为2,焦点与椭圆+=1的焦点相同,那么双曲线的焦点坐标为　　　　;渐近线方程为　　　　. 

    查看答案和解析>>

    同步练习册答案