练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知某产品连续4个月的广告费用xi(千元)与销售额yi(万元)，经过对这些数据的处理，得到如下数据信息：；②广告费用x和销售额y之间具有较强的线性相关关系；③回归直线方程(用最小二乘法求得)．则当广告费用为6千元时，可预测销售额约为(　　)

    A．3.5万元                              B．4.7万元 

    C．4.9万元                              D．6.5万元


    B

    [解析]　回归直线必过样本点的中心＝3.5，∴3.5＝


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知直角坐标系内的两个向量a＝(1,3)，b＝(m,2m－3)使平面内的任意一个向量c都可以唯一地表示成c＝λa＋μb，则m的取值范围是(　　)

    A．(－∞，0)∪(0，＋∞)                 B．(－∞，－3)∪(－3，＋∞)

    C．(－∞，3)∪(3，＋∞)                 D．[－3,3)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    “m＝”是“直线(m＋2)x＋3my＋1＝0与直线(m－2)x＋(m＋2)y－3＝0互相垂直”的(　　)

    A．充要条件                             B．充分不必要条件

    C．必要不充分条件                       D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知△ABC的三个顶点为A(－1,0)，B(1,0)，C(3,2)，其外接圆为⊙H.

    (1)若直线l过点C，且被⊙H截得的弦长为2，求直线l的方程；

    (2)对于线段BH上的任意一点P，若在以C为圆心的圆上都存在不同的两点M，N，使得点M是线段PN的中点，求⊙C的半径r的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一个样本a,3,5,7的平均数是b，且a，b是方程x2－5x＋4＝0的两根，则这个样本的方差是(　　)

    A．3                                    B．4 

    C．5                                    D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明，得到如下列联表：

    性别与是否读营养说明列联表

     

    男

    女

    总计

    读营养说明

    16

    8

    24

    不读营养说明

    4

    12

    16

    总计

    20

    20

    40

    (1)根据以上列联表进行独立性检验，能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系？

    (2)从被询问的16名不读营养说明的大学生中，随机抽取2名学生，求抽到男生人数ξ的分布列及其均值(即数学期望)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    △ABC中，若sin2A=sin2B+sin2C，则△ABC为(    )

       A．直角三角形                B． 钝三角形

       C．锐角三角形               D．锐角或直角三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知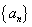是等差数列，其前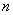项和为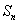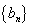，是等比数列，且，，．

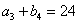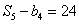    （1）求数列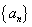与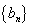的通项公式；

    （2）对任意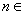N，是否存在正实数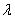，使不等式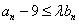恒成立，若存在，求出 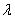的最小值，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数是奇函数，则实数的值为         ．

    查看答案和解析>>

    同步练习册答案