
分析 (1)设G(ρ1,θ),H(ρ2,θ+$\frac{π}{2}$),则(ρ1cosθ)2+2(ρ1sinθ)2=2,ρ12=$\frac{2}{co{s}^{2}θ+2si{n}^{2}θ}$.同理ρ22=$\frac{2}{si{n}^{2}θ+2co{s}^{2}θ}$,利用$\frac{1}{O{H}^{2}}$+$\frac{1}{O{G}^{2}}$=$\frac{1}{{{ρ}_{1}}^{2}}$+$\frac{1}{{{ρ}_{2}}^{2}}$,即可证明结论;
(2)假设存在满足条件的定圆,设圆的半径为R,则OG•OH=R•GH,求出半径,即可得出结论.
解答 解:(1)设G(ρ1,θ),H(ρ2,θ+$\frac{π}{2}$),则(ρ1cosθ)2+2(ρ1sinθ)2=2,
∴ρ12=$\frac{2}{co{s}^{2}θ+2si{n}^{2}θ}$.
同理ρ22=$\frac{2}{si{n}^{2}θ+2co{s}^{2}θ}$,
∴$\frac{1}{O{H}^{2}}$+$\frac{1}{O{G}^{2}}$=$\frac{1}{{{ρ}_{1}}^{2}}$+$\frac{1}{{{ρ}_{2}}^{2}}$=$\frac{1+2}{2}$=$\frac{3}{2}$;
另解:当OG,OH有一个不存在时,显然有1+$\frac{1}{2}$=$\frac{3}{2}$;
设直线OH:y=kx,代入椭圆方程,可得x2=$\frac{2}{1+2{k}^{2}}$,y2=$\frac{2{k}^{2}}{1+2{k}^{2}}$,
$\frac{1}{O{H}^{2}}$=$\frac{1}{{x}^{2}+{y}^{2}}$=$\frac{1+2{k}^{2}}{2(1+{k}^{2})}$,
将k换成-$\frac{1}{k}$,可得$\frac{1}{O{G}^{2}}$=$\frac{2+{k}^{2}}{2(1+{k}^{2})}$,
则$\frac{1}{O{H}^{2}}$+$\frac{1}{O{G}^{2}}$=$\frac{3+3{k}^{2}}{2+2{k}^{2}}$=$\frac{3}{2}$.
(2)假设存在满足条件的定圆,设圆的半径为R,则OG•OH=R•GH
∵OG2+OH2=GH2,∴$\frac{1}{O{H}^{2}}$+$\frac{1}{O{G}^{2}}$=$\frac{1}{{R}^{2}}$=$\frac{3}{2}$,
∴满足条件的定圆方程为:x2+y2=$\frac{2}{3}$.
点评 本题考查了椭圆的标准方程,考查了直线与圆锥曲线的关系,考查了数学转化思想方法,属于中档题.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:选择题
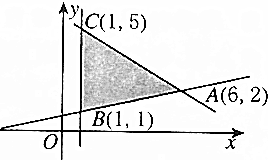 给出平面可行域(如图),若使目标函数z=ax+y取最大值的最优解有无穷多个,则a=( )
给出平面可行域(如图),若使目标函数z=ax+y取最大值的最优解有无穷多个,则a=( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | 4 | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要的条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com