
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,如果方程
时,如果方程![]() 有两个不等实根
有两个不等实根![]()
![]() ,求实数t的取值范围,并证明
,求实数t的取值范围,并证明![]() .
.
【答案】(1)当![]() 时,
时,![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;当
;当![]() 时,
时,![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(2)
;(2)![]() ,证明见解析.
,证明见解析.
【解析】
(1)求出![]() ,对
,对![]() 分类讨论,分别求出
分类讨论,分别求出![]() 的解,即可得出结论;
的解,即可得出结论;
(2)由(1)得出![]() 有两解时
有两解时![]() 的范围,以及
的范围,以及![]() 关系,将
关系,将![]() ,等价转化为证明
,等价转化为证明![]() ,不妨设
,不妨设![]() ,令
,令![]() ,则
,则![]()
![]() ,即证
,即证![]() ,构造函数
,构造函数![]() ,只要证明对于任意
,只要证明对于任意![]() 恒成立即可.
恒成立即可.
(1)![]() 的定义域为R,且
的定义域为R,且![]() .
.
由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() .
.
故当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,
,
单调递减区间是![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,
,
单调递减区间是![]() .
.
(2)由(1)知当![]() 时,
时,![]() ,且
,且![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
![]() 当
当![]() 时,直线
时,直线![]() 与
与![]() 的图像有两个交点,
的图像有两个交点,
![]() 实数t的取值范围是
实数t的取值范围是![]() .
.
![]() 方程
方程![]() 有两个不等实根
有两个不等实根![]()
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,即
,即![]() .
.
要证![]() ,只需证
,只需证![]() ,
,
即证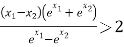 ,不妨设
,不妨设![]() .
.
令![]() ,则
,则![]()
![]() ,
,
则要证![]() ,即证
,即证![]() .
.
令![]() ,则
,则![]() .
.
令![]() ,则
,则![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,![]() .
.
![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,即
,即![]() 成立,
成立,
即![]() 成立.
成立.![]() .
.


科目:高中数学 来源: 题型:
【题目】已知某公司生产某产品的年固定成本为100万元,每生产1千件需另投入27万元,设该公司一年内生产该产品![]() 千件
千件![]() 并全部销售完,每千件的销售收入为
并全部销售完,每千件的销售收入为![]() 万元,且
万元,且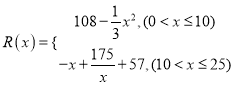 .
.
⑴ 写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
⑵ 当年产量为多少千件时,该公司在这一产品的生产中所获年利润最大?(注:年利润=年销售收入![]() 年总成本).
年总成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ,Q为l上的动点,以OQ为边作等边三角形OPQ,且三点O,P,Q按逆时针方向排列.
,Q为l上的动点,以OQ为边作等边三角形OPQ,且三点O,P,Q按逆时针方向排列.
(Ⅰ)设点P运动轨迹E的直角坐标方程;
(Ⅱ)若曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,若点M为曲线
,若点M为曲线![]() 上的动点,且点M到曲线E的最小距离为1,求实数a的值.
上的动点,且点M到曲线E的最小距离为1,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于集合![]() ,
,![]() ,
,![]() ,
,![]() ,定义
,定义![]() .
.
集合![]() 中的元素个数记为
中的元素个数记为![]() ,当
,当![]() ,称集合
,称集合![]() 具有性质
具有性质![]() .
.
(1)已知集合![]() ,
,![]() ,写出
,写出![]() ,
,![]() 的值,并判断集合
的值,并判断集合![]() 是否具有性质
是否具有性质![]() ;
;
(2)设集合![]() 具有性质
具有性质![]() ,判断集合
,判断集合![]() 中的三个元素是否能组成等差数列,请说明理由;
中的三个元素是否能组成等差数列,请说明理由;
(3)若数列![]() 是以
是以![]() 为首项,2为公比的等比数列. 数列
为首项,2为公比的等比数列. 数列![]() 中的前100项:
中的前100项:![]() 组成的集合
组成的集合![]() 记作
记作![]() ,将集合
,将集合![]() 中的所有元素
中的所有元素![]() 从小到大排序,即
从小到大排序,即![]() 满足
满足![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着夏季的到来,冰枕成为市面上的一种热销产品,某厂家为了调查冰枕在当地大学的销售情况,作出调研,并将所得数据统计如下表所示:
表一:
温度在30℃以下 | 温度在30℃以上 | 总计 | |
女生 | 10 | 30 | 40 |
男生 | 40 | 20 | 60 |
总计 | 50 | 50 | 100 |
随后在该大学一个小卖部调查了冰枕的出售情况,并将某月的日销售件数(x)与销售天数(y)统计如下表所示:
表二:
第 | 2 | 4 | 6 | 8 | 10 |
| 3 | 6 | 7 | 10 | 12 |
(1)请根据表二中的数据在下列网格纸中绘制散点图;
(2)请根据表二中提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)从(1)(2)中的数据及回归方程我们可以得到,销售件数随着销售天数的增长而增长,但无法判断男、女生对冰枕的选择是否与温度有关,请结合表一中的数据,并自己设计方案来判段是否有99.9%的可能性说明购买冰枕的性别与温度相关.
参考数据及公式:
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
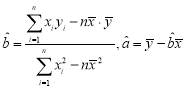 ;
;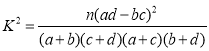 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com