
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
分析 利用公式求出$\hat{b}$,$\hat{a}$,即可得出结论.
解答 解:样本平均数$\overline{x}$=$\frac{1}{5}(2+4+5+6+8)$=5,$\overline{y}$=$\frac{1}{5}(30+40+60+50+70)$=50.
∴$\sum _{i=1}^{6}$(xi-$\overline{x}$)(yi-$\overline{y}$)=-3×(-20)+(-1)×(-10)+0+0+3×20=130,
$\sum _{i=1}^{6}$ (xi-$\overline{x}$)2=9+1+0+1+9=20,
∴$\hat{b}$=$\frac{130}{20}=6.5$,
∴$\hat{a}$=50-6.5×5=7.5.
线性回归方程为:y=6.5x+17.5,
预测当广告费为7百万元时,即x=7时,y=63百万元.
故答案为:6300.
点评 本题考查线性回归方程的求法,考查最小二乘法,属于基础题


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 1 | D. | $\frac{15}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
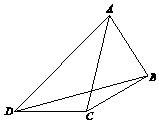 在如图所示的平面图形中,已知CD=$\sqrt{2}$,∠BCA=45°,∠ACD=105°,∠CDB=15°,∠BDA=30°.
在如图所示的平面图形中,已知CD=$\sqrt{2}$,∠BCA=45°,∠ACD=105°,∠CDB=15°,∠BDA=30°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “p或q”为真,“非q”为假 | B. | “p且q”为假,“非p”为假 | ||
| C. | “p且q”为假,“非p”为真 | D. | “p且q”为假,“p或q”为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图在△ABC中,∠BAC=120°,AB=1,AC=2,D为BC边上一点(含端点),$\overrightarrow{DC}=λ\overrightarrow{BD}(λ≥0)$,则$\overrightarrow{AD}•\overrightarrow{BC}$的最大值为( )
如图在△ABC中,∠BAC=120°,AB=1,AC=2,D为BC边上一点(含端点),$\overrightarrow{DC}=λ\overrightarrow{BD}(λ≥0)$,则$\overrightarrow{AD}•\overrightarrow{BC}$的最大值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com