
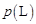 关于行驶速度
关于行驶速度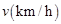 的函数解析式可以表示为:
的函数解析式可以表示为: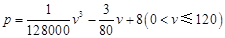 .已知甲、乙两地相距
.已知甲、乙两地相距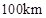 ,设汽车的行驶速度为
,设汽车的行驶速度为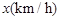 ,从甲地到乙地所需时间为
,从甲地到乙地所需时间为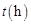 ,耗油量为
,耗油量为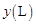 .
.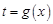 及
及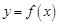 ;
;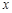 为多少时,
为多少时,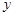 取得最小值,并求出这个最小值.
取得最小值,并求出这个最小值. 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源:不详 题型:解答题
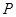 (元)与时间
(元)与时间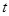 (天)所组成的有序数对
(天)所组成的有序数对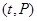 落在下图中的两条线段上,该股票在30天内的日交易量
落在下图中的两条线段上,该股票在30天内的日交易量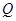 (万股)与时间
(万股)与时间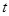 (天)的部分数据如下表所示.
(天)的部分数据如下表所示.
| 第t天 | 4 | 10 | 16 | 22 |
| Q(万股) | 36 | 30 | 24 | 18 |
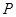 (元)与时间
(元)与时间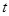 (天)所满足的函数关系式;
(天)所满足的函数关系式;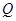 (万股)与时间
(万股)与时间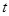 (天)的一次函数关系式;
(天)的一次函数关系式; (万元)表示该股票日交易额,写出
(万元)表示该股票日交易额,写出 关于
关于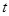 的函数关系式,并求这30天中第几天日交易额最大,最大值为多少?
的函数关系式,并求这30天中第几天日交易额最大,最大值为多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
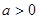 ,函数
,函数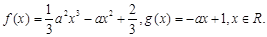
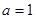 时,求函数
时,求函数 在点(1,
在点(1,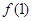 )的切线方程;
)的切线方程; 在[-1,1]的极值;
在[-1,1]的极值;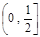 上至少存在一个实数x0,使
上至少存在一个实数x0,使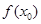 >g(xo)成立,求正实数
>g(xo)成立,求正实数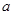 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
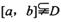 和常数c,使得对任意x1
和常数c,使得对任意x1 ,都有
,都有 ,且对任意x2
,且对任意x2 D,当
D,当 时,
时, 恒成立,则称函数f(x)为区间D上的“平顶型”函数.给出下列说法:
恒成立,则称函数f(x)为区间D上的“平顶型”函数.给出下列说法: 为R上的“平顶型”函数;
为R上的“平顶型”函数; 时,函数,
时,函数, 是区间
是区间 上的“平顶型”函数.
上的“平顶型”函数.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com