
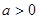 ,函数
,函数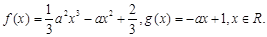
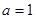 时,求函数
时,求函数 在点(1,
在点(1,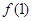 )的切线方程;
)的切线方程; 在[-1,1]的极值;
在[-1,1]的极值;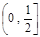 上至少存在一个实数x0,使
上至少存在一个实数x0,使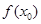 >g(xo)成立,求正实数
>g(xo)成立,求正实数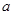 的取值范围。
的取值范围。 在点(1,
在点(1,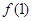 )的切线方程为
)的切线方程为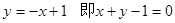
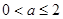 时,极大值为
时,极大值为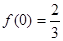 ,无极小值
,无极小值 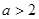 时 极大值是
时 极大值是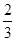 ,极小值是
,极小值是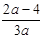
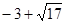
 ,
,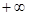 )
)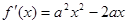 ,那么当
,那么当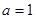 时,
时,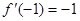 又
又 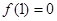 所以函数
所以函数 在点(1,
在点(1,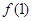 )的切线方程为
)的切线方程为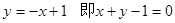 ;(2)中令
;(2)中令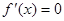 有
有 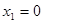
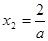
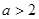 ,和
,和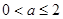 得到极值。(3)中,设
得到极值。(3)中,设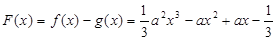 ,
,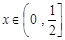 ,依题意,只需
,依题意,只需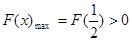 那么可以解得。
那么可以解得。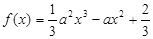 ∴
∴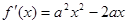
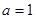 时,
时,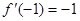 又
又 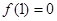
 在点(1,
在点(1,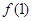 )的切线方程为
)的切线方程为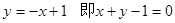 --------4分
--------4分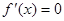 有
有 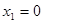
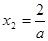
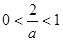 即
即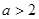 时
时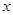 | (-1,0) | 0 | (0,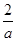 ) ) | 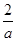 | (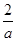 ,1) ,1) |
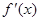 | + | 0 | - | 0 | + |
 |  | 极大值 |  | 极小值 |  |
 的极大值是
的极大值是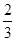 ,极小值是
,极小值是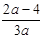
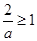 即
即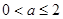 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为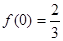 ,无极小值。
,无极小值。 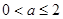 时,极大值为
时,极大值为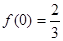 ,无极小值
,无极小值 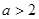 时 极大值是
时 极大值是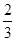 ,极小值是
,极小值是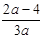 ----------8分
----------8分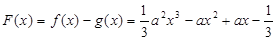 ,
,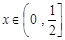
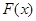 求导,得
求导,得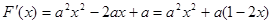
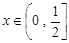 ,
,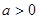
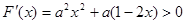
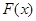 在区间
在区间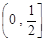 上为增函数,则
上为增函数,则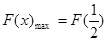
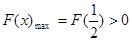 ,即
,即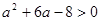
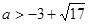 或
或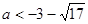 (舍去)
(舍去)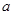 的取值范围是(
的取值范围是(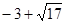
 ,
,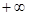 )
)

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:单选题
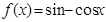 ;②
;②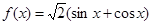 ;③
;③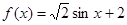 ;④
;④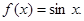 其中“互为生成函数”的是( )
其中“互为生成函数”的是( )| A.①② | B.①③ | C.③④ | D.②④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
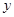 随自变量
随自变量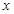 变化的一组数据,由此可判断它最可能的函数模型为
变化的一组数据,由此可判断它最可能的函数模型为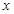 |  |  | 0 | 1 | 2 | 3 |
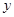 |  |  | 1 | 4 | 16 | 64 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
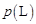 关于行驶速度
关于行驶速度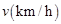 的函数解析式可以表示为:
的函数解析式可以表示为: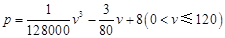 .已知甲、乙两地相距
.已知甲、乙两地相距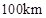 ,设汽车的行驶速度为
,设汽车的行驶速度为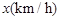 ,从甲地到乙地所需时间为
,从甲地到乙地所需时间为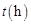 ,耗油量为
,耗油量为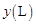 .
.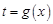 及
及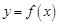 ;
;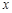 为多少时,
为多少时,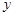 取得最小值,并求出这个最小值.
取得最小值,并求出这个最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com