练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    用0、1、2、3、4、5组成一个无重复数字的五位数，这个数是偶数的概率为     。

    试题分析： 选个数全排，再减去首位为的，可得组成的无重复数字五位数的个数为，这个数是偶数包括三种情况：末尾为，末尾为的有种情况，末尾为的各有种情况，这个数是偶数的概率为。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    以下茎叶图记录了甲、乙两组各三名同学在期末考试的数学成绩，乙组记录中有一个数字模糊，无法确认．假设这个数字具有随机性，并在图中以a表示．
    （1）若甲、乙两个小组的数学平均成绩相同，求a的值；
    （2）求乙组平均成绩超过甲组平均成绩的概率；
    （3）当a=2时，分别从甲、乙两组中各随机选取一名同学，设这两名同学成绩之差的绝对值为X，求随机变量X的分布列和数学期望，

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

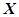    一个袋中装有8个大小质地相同的球，其中4个红球、4个白球，现从中任意取出四个球，设为取得红球的个数．
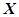    （1）求的分布列；
    （2）若摸出4个都是红球记5分，摸出3个红球记4分，否则记2分．求得分的期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某种产品的广告费支出额x与销售额y（单位：万元）之间有如下对应数据：
    x24568
    y3040605070
    （1）求y关于x的回归直线方程；
    （2）试预测广告费支出为10万元时，销售额多大？
    （参考公式：回归直线方程a，其中b=
    n
    i=1
    xiyi-n
    .
    x
    .
    y
    n
    i=1
    xi2-nx-2
    ）．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    一张方桌的图案如图所示，将一颗豆子随机地扔到桌面上，假设豆子不落在线上，下列事件的概率：

    （1）豆子落在红色区域概率为；
    （2）豆子落在黄色区域概率为；
    （3）豆子落在绿色区域概率为；
    （4）豆子落在红色或绿色区域概率为；
    （5）豆子落在黄色或绿色区域概率为.
    其中正确的结论有（   ）
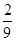    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

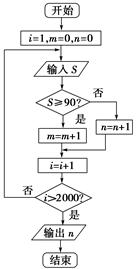
    如图是统计高三年级2 000名同学某次数学考试成绩的程序框图，S代表分数，若输出的结果是560，则这次考试数学分数不低于90分的同学的概率是(  )
    A．0.28 B．0.38 C．0.72D．0.62

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某工厂生产A，B两种元件，其质量按测试指标划分，指标大于或等于82为正品，小于82为次品．现随机抽取这两种元件各100个进行检测，检测结果统计如下：
    测试
    指标
    		[70,76)
    		[76,82)
    		[82,88)
    		[88,94)
    		[94,100]
    元件A
    		8
    		12
    		40
    		32
    		8
    元件B
    		7
    		18
    		40
    		29
    		6
    (1)试分别估计元件A，元件B为正品的概率；
    (2)生产1个元件A，若是正品则盈利40元，若是次品则亏损5元；生产1个元件B，若是正品则盈利50元，若是次品则亏损10元．在(1)的前提下，
    (ⅰ)X为生产1个元件A和1个元件B所得的总利润，求随机变量X的分布列和数学期望；
    (ⅱ)求生产5个元件B所得利润不少于140元的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    甲、乙、丙三名音乐爱好者参加某电视台举办的演唱技能海选活动，在本次海选中有合格和不合格两个等级．若海选合格记分，海选不合格记分．假设甲、乙、丙海选合格的概率分别为，他们海选合格与不合格是相互独立的．
    （1）求在这次海选中，这三名音乐爱好者至少有一名海选合格的概率；
    （2）记在这次海选中，甲、乙、丙三名音乐爱好者所得分之和为随机变量,求随机变量的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    某人一周晚上值班2次，在已知他周日一定值班的条件下，他在周六晚上值班的概率为________．

    查看答案和解析>>

    同步练习册答案