
分析 (1)结合已知中S=a2-(b-c)2和余弦定理得:sinA=4-4cosA,又由sin2A+cos2A=1,消去余弦,解得sinA;
(2)由b+c=6,结合三角形面积公式和基本不等式,可得△ABC的面积的最大值.
解答 解:(1)∵S=a2-(b-c)2=a2-b2-c2+2bc=$\frac{1}{2}$bcsinA:
又由余弦定理得:a2-b2-c2=-2bccosA,
∴-2bccosA+2bc=$\frac{1}{2}$bcsinA,
即sinA=4-4cosA,
又由sin2A+cos2A=1,
∴sin2A+(1-$\frac{1}{4}$sinA)2=1,
解得:sinA=$\frac{8}{17}$,或sinA=0(舍去);
(2)∵b+c=6,
∴S=$\frac{1}{2}$bcsinA=$\frac{4}{17}$bc≤$\frac{4}{17}$($\frac{b+c}{2}$)2=$\frac{36}{17}$,
当且令当b=c=3时取等号,
即△ABC的面积的最大值为$\frac{36}{17}$.
点评 本题考查的知识点是三角形面积公式,余弦定理,基本不等式,是基本不等式与解三角形的综合应用,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 品种甲 | 403 | 397 | 390 | 404 | 388 | 400 | 412 | 406 |
| 品种乙 | 419 | 403 | 412 | 418 | 408 | 423 | 400 | 413 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2$\sqrt{5}$ | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
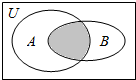
| A. | {x|-4<x<-2} | B. | {x|-4<x<0} | C. | {x|x>0} | D. | {x|x<-2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | {-1,0,1} | C. | (0,2) | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
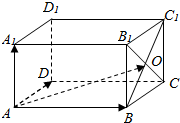 如图,在平行六面体ABCD-A1B1C1D1中,B1C∩BC1=O,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=2.
如图,在平行六面体ABCD-A1B1C1D1中,B1C∩BC1=O,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com