
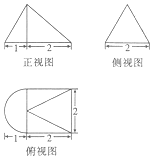
 某几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的表面积为( )
某几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的表面积为( )| A. | $\frac{(8+π)\sqrt{3}}{2}$ | B. | $\frac{(8+π)\sqrt{3}}{6}$ | C. | $\frac{π}{2}$+4+$\frac{5}{2}$$\sqrt{3}$ | D. | $\frac{3}{2}$π+8+$\sqrt{7}$ |
分析 由已知的三视图可得:该几何体是一个半圆锥与一个四棱锥组合而成的几何体,进而可得答案.
解答 解:由已知的三视图可得:该几何体是一个半圆锥与一个四棱锥组合而成的几何体,
其表面积由半圆锥的曲面,底面及四棱锥的底面,前,后,右侧面组成,
∵其侧视图是一个等边三角形,
∴半圆锥的底面半径为1,高为$\sqrt{3}$,故圆锥的母线长为:2,
故半圆锥的底面面积为:$\frac{1}{2}π$,曲侧面面积为:π,
四棱锥的底面面积为:4,
前后侧面均为腰长为2的等腰直角三角形,面积均为:2,
右侧面是腰为2$\sqrt{2}$,底为2的等腰三角形,面积为:$\sqrt{7}$,
故组合体的表面积为:$\frac{3}{2}$π+8+$\sqrt{7}$,
故选:D
点评 本题考查的知识点是棱锥的体积和表面积,圆锥的体积和表面积,简单几何体的三视图,难度中档.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
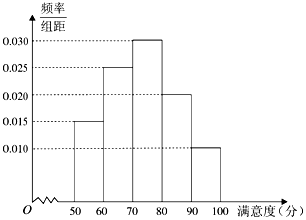 某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表:
某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表:| 满意度 评分分组 | 频数 |
| [50,60) | 2 |
| [60,70) | 8 |
| [70,80) | 14 |
| [80,90) | 14 |
| [90,100] | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-3,2} | B. | {-3,0,2} | C. | {3,-2} | D. | {3,0,-2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{55}{29}$] | B. | (1,$\frac{31}{21}$] | C. | [$\frac{31}{21}$,+∞) | D. | [$\frac{55}{29}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,单位位圆上的两个向量$\overrightarrow{a},\overrightarrow{b}$相互垂直,若向量$\overrightarrow{c}$满足($\overrightarrow{c}-\overrightarrow{a}$)•($\overrightarrow{c}-\overrightarrow{b}$)=0,则|$\overrightarrow{c}$|的取值范围是( )
如图所示,单位位圆上的两个向量$\overrightarrow{a},\overrightarrow{b}$相互垂直,若向量$\overrightarrow{c}$满足($\overrightarrow{c}-\overrightarrow{a}$)•($\overrightarrow{c}-\overrightarrow{b}$)=0,则|$\overrightarrow{c}$|的取值范围是( )| A. | [0,1] | B. | [0,$\sqrt{2}$] | C. | [1,$\sqrt{2}$] | D. | [1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com