
| A. | (1,$\frac{55}{29}$] | B. | (1,$\frac{31}{21}$] | C. | [$\frac{31}{21}$,+∞) | D. | [$\frac{55}{29}$,+∞) |
分析 根据对数运算性质可得$\frac{y}{x}$=3m,令$\frac{y}{x}$=t,则不等式可化简为2(a+1)t2-16t+3a-1≥0,令f(t)=2(a+1)t2-16t+3a-1,则问题转化为fmax(t)≥0,讨论对称轴与开口方向,根据二次函数的性质求出fmax(t)即可得出a的范围.
解答 解:∵log${\;}_{\frac{1}{3}}$x+log3y=m,即log3$\frac{1}{x}$+log3y=log3$\frac{y}{x}$=m,
∴$\frac{y}{x}$=3m,∵m∈[-1,1],∴$\frac{y}{x}$∈[$\frac{1}{3}$,3].
∵3ax2-18xy+(2a+3)y2≥(x-y)2,
∴3a-18$\frac{y}{x}$+(2a+3)$\frac{{y}^{2}}{{x}^{2}}$≥1-2$\frac{y}{x}$+$\frac{{y}^{2}}{{x}^{2}}$,
令$\frac{y}{x}$=t,则2(a+1)t2-16t+3a-1≥0,
设f(t)=2(a+1)t2-16t+3a-1,
∵不等式3ax2-18xy+(2a+3)y2≥(x-y)2有解,
∴f(t)在[$\frac{1}{3}$,3]上的最大值fmax(x)≥0,
(1)当a=-1时,f(t)=-16t-4,
∴fmax(t)=f($\frac{1}{3}$)=-$\frac{16}{3}$-4<0,不符合题意;
(2)若a<-1,则f(t)开口向下,对称轴为t=$\frac{4}{a+1}$<0,
∴f(t)在[$\frac{1}{3}$,3]上单调递减,
∴fmax(t)=f($\frac{1}{3}$)=$\frac{29a}{9}$-6<0,不符合题意;
(3)若a>-1,则f(t)开口向上,对称轴为t=$\frac{4}{a+1}$>0,
(i)若0<$\frac{4}{a+1}$≤$\frac{1}{3}$,即a≥11时,f(t)在[$\frac{1}{3}$,3]上单调递增,
∴fmax(t)=f(3)=21a-31>0,符合题意;
(ii)若$\frac{4}{a+1}≥3$,即-1<a$≤\frac{1}{3}$时,f(t)在[$\frac{1}{3}$,3]上单调递减,
∴fmax(t)=f($\frac{1}{3}$)=$\frac{29a}{9}$-6≤$\frac{29}{27}$-6<0,不符合题意;
(iii)若$\frac{1}{3}$<$\frac{4}{a+1}$<3,即$\frac{1}{3}$<a<11时,f(t)在[$\frac{1}{3}$,3]上先减后增,
∴fmax(t)=f($\frac{1}{3}$)或fmax(t)=f(3),
∴f($\frac{1}{3}$)=$\frac{29a}{9}$-6≥0或f(3)=21a-31>0,
解得a≥$\frac{54}{29}$或a≥$\frac{31}{21}$,又$\frac{1}{3}$<a<11,
∴$\frac{31}{21}$≤a<11,
综上,a的取值范围是[$\frac{31}{21}$,+∞).
故选C.
点评 本题考查了二次函数的性质,对数的运算性质,函数最值的计算及函数存在性问题,属于中档题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 36 | C. | 81 | D. | 41 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{e}$,e] | B. | [-$\frac{2}{e}$,2e] | C. | $(-\frac{2}{e},2e)$ | D. | $[-\frac{3}{e},3e]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{13}}}{2}$ | B. | $\frac{3}{2}$ | C. | $1+\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
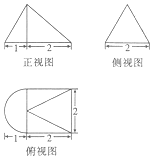 某几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的表面积为( )
某几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的表面积为( )| A. | $\frac{(8+π)\sqrt{3}}{2}$ | B. | $\frac{(8+π)\sqrt{3}}{6}$ | C. | $\frac{π}{2}$+4+$\frac{5}{2}$$\sqrt{3}$ | D. | $\frac{3}{2}$π+8+$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
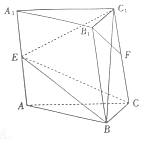 如图,已知直三棱柱ABC-A1B1C1的底面是边长为4的正三角形,B,E,F分别是AA1,CC1的中点,且BE⊥B1F.
如图,已知直三棱柱ABC-A1B1C1的底面是边长为4的正三角形,B,E,F分别是AA1,CC1的中点,且BE⊥B1F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
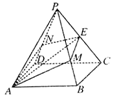 如图,在正四棱锥P-ABCD中,AB=2,PA=$\sqrt{6}$,E是棱PC的中点,过AE作平面分别与棱PB、PD交于M、N两点.
如图,在正四棱锥P-ABCD中,AB=2,PA=$\sqrt{6}$,E是棱PC的中点,过AE作平面分别与棱PB、PD交于M、N两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com