
| A. | [-$\frac{1}{e}$,e] | B. | [-$\frac{2}{e}$,2e] | C. | $(-\frac{2}{e},2e)$ | D. | $[-\frac{3}{e},3e]$ |
分析 求出g(x)的反函数h(x),则g(x)与f(x)的图象在[$\frac{1}{e}$,e2]上有交点,借助函数图象及导数的几何意义即可求出k的范围.
解答 解:g(x)=($\frac{1}{e}$)${\;}^{\frac{x}{2}}$=(e${\;}^{-\frac{1}{2}}$)x关于直线y=x的对称函数为h(x)=log${\;}_{{e}^{-\frac{1}{2}}}$x=-2lnx,
则y=h(x)与y=f(x)=kx在[$\frac{1}{e}$,e2]上有交点,
作出y=h(x)与y=f(x)在[$\frac{1}{e}$,e2]上的函数图象如图所示: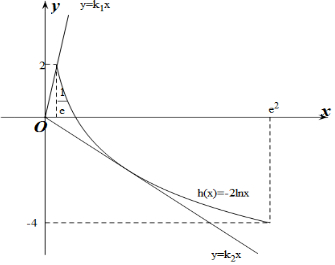
设y=k1x经过点($\frac{1}{e}$,2),则k1=2e,
设y=k2x与h(x)=-2lnx相切,切点为(x0,y0),
则$\left\{\begin{array}{l}{-\frac{2}{{x}_{0}}={k}_{2}}\\{{k}_{2}{x}_{0}=-2ln{x}_{0}}\end{array}\right.$,解得x0=e,k2=-$\frac{2}{e}$.
∴$-\frac{2}{e}$≤k≤2e.
故选B.
点评 本题考查了函数零点与函数图象的关系,将对称问题转化为交点问题是解题关键,属于中档题.


 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:解答题
 团购已成为时下商家和顾客均非常青睐的一种省钱、高效的消费方式,不少商家同时加入多家团购网,现恰有三个团购网站在A市开展了团购业务,A市某调查公司为调查这三家团购网站在本市的开展情况,从本市已加入了团购网站的商家中随机地抽取了50家进行调查,他们加入这三家团购网站的情况如下图所示.
团购已成为时下商家和顾客均非常青睐的一种省钱、高效的消费方式,不少商家同时加入多家团购网,现恰有三个团购网站在A市开展了团购业务,A市某调查公司为调查这三家团购网站在本市的开展情况,从本市已加入了团购网站的商家中随机地抽取了50家进行调查,他们加入这三家团购网站的情况如下图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
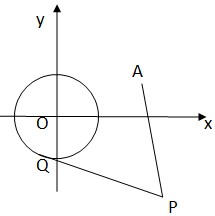 已知圆O:x2+y2=1和定点A(2,1),由圆外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|.
已知圆O:x2+y2=1和定点A(2,1),由圆外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-3,2} | B. | {-3,0,2} | C. | {3,-2} | D. | {3,0,-2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{55}{29}$] | B. | (1,$\frac{31}{21}$] | C. | [$\frac{31}{21}$,+∞) | D. | [$\frac{55}{29}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2}{3}$) | B. | (0,$\frac{1}{2}$] | C. | [$\frac{1}{3}$,1) | D. | [$\frac{1}{2}$,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com