
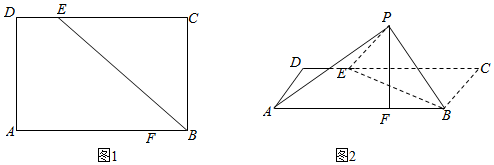
分析 (1)连结EF,由翻折不变性可知,PB=BC=6,PE=CE=9,由已知条件,利用勾股定理推导出PF⊥BF,PF⊥EF,由此能够证明PF⊥平面ABED.
(2)由PF⊥平面ABED,知PF为三棱锥P-ABE的高,利用等积法能求出点A到平面PBE的距离.
解答 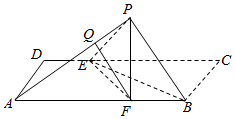 解:(1)连结EF,
解:(1)连结EF,
由翻折不变性可知,PB=BC=6,PE=CE=9,
在△PBF中,PF2+BF2=20+16=36=PB2,
所以PF⊥BF…(2分)
在图1中,利用勾股定理,得EF=$\sqrt{{6}^{2}+(12-3-4)^{4}}$=$\sqrt{61}$,
在△PEF中,EF2+PF2=61+20=81=PE2,
∴PF⊥EF…(4分)
又∵BF∩EF=F,BF?平面ABED,EF?平面ABED,
∴PF⊥平面ABED.…(6分)
(2)解:由(1)知PF⊥平面ABED,
∴PF为三棱锥P-ABE的高.…(8分)
设点A到平面PBE的距离为h,
由等体积法得VA-PBE=VP-ABE,…(10分)
即$\frac{1}{3}×\frac{1}{2}×6×9×h=\frac{1}{3}×\frac{1}{2}×12×6×2\sqrt{5}$
∴h=$\frac{8\sqrt{5}}{3}$,
即点A到平面PBE的距离为$\frac{8\sqrt{5}}{3}$.…(14分)
点评 本题考查直线与平面垂直的证明,考查点到平面距离的求法,解题时要注意空间思维能力的培养,要注意等积法的合理运用.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
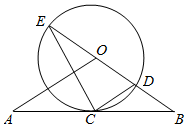 如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于点E、D,连接EC,CD.若tan∠CED=$\frac{1}{2}$,⊙O的半径为3.
如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于点E、D,连接EC,CD.若tan∠CED=$\frac{1}{2}$,⊙O的半径为3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 数学成绩 物理成绩 | 优秀 | 不优秀 | 合计 |
| 优秀 | 5 | 2 | 7 |
| 不优秀 | 1 | 12 | 13 |
| 合计 | 6 | 14 | 20 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∨q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
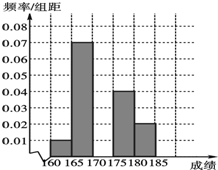 北京某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
北京某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [160,165) | 5 | 0.050 |
| 第2组 | [165,170) | n | 0.350 |
| 第3组 | [170,175) | 30 | p |
| 第4组 | [175,180) | 20 | 0.200 |
| 第5组 | [180,185] | 10 | 0.100 |
| 合计 | 100 | 1.000 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com