
分析 ①根据正态分布的对称性,求出P(ξ>2),进行判断;
②根据相互独立事件概率计算公式,求出他在接下来的6次测验中,恰好前4次及格的概率,进行判断;
③根据复数的概念以及充分条件和必要条件的定义进行判断;
④根据命题的推理关系进行判断;
⑤根据积分的几何意义进行求解.
解答 解:①已知随机变量ξ服从正态分布N(0,σ2),且P(-2≤ξ≤2)=0.9,则P(0≤ξ≤2)=0.45,则P(ξ>2)=0.5-0.45=0.05;故①正确,
②某学生在最近的15次数学测验中有5次不及格,故他每次考试及格的概率P=$\frac{15-5}{15}$=$\frac{2}{3}$,不及格的概率P=$\frac{5}{15}$=$\frac{1}{3}$,
故按照这个成绩,他在接下来的6次测验中,恰好前4次及格的概率为($\frac{2}{3}$)4($\frac{1}{3}$)2,故②正确;
③设a,b∈R,若a=0,则a+bi=bi,不一定是纯虚数,即充分性不成立,反之,若复数a+bi是纯虚数,则a=0且b≠0,则必要性成立,
即“a=0”是“复数a+bi是纯虚数”的必要不充分条件,故③正确,
④当n=5时如果命题成立,则推得当n=6时,命题也成立,但如果当n=5时该命题不成立,则无法推得当n=6时,该命题是否成立,故④错误;
⑤由曲线y=x2-1与直线x=2,y=0所围成的区域的面积为:${∫}_{1}^{2}({x}^{2}-1)dx$=$(\frac{1}{3}{x}^{3}-x){|}_{1}^{2}$=$\frac{4}{3}$;故⑤正确,
故答案为:①②③⑤
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,有一定的难度.


科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-∞,1) | C. | (0,+∞) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{π}^{2}}{4}$+1 | B. | $\frac{{π}^{2}}{4}$-1 | C. | $\frac{3{π}^{2}}{8}$-1 | D. | $\frac{3{π}^{2}}{8}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 使用年数 | 2 | 4 | 6 | 8 | 10 |
| 售价 | 16 | 13 | 9.5 | 7 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
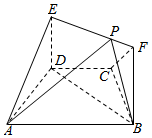 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com