
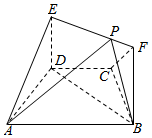
 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1分析 (Ⅰ)推导出AD⊥BD,DE⊥DB,从而DE⊥平面ABCD,进而DE⊥AD,由此能证明AD⊥平面BFED.
(Ⅱ)分别以直线DA,DB,DE为x轴,y轴,z轴的,建立空间直角坐标系,利用向量法能求出θ的最小值.
解答 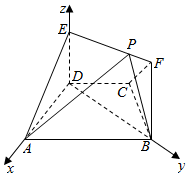 证明:(Ⅰ)在梯形ABCD中,
证明:(Ⅰ)在梯形ABCD中,
∵AB∥CD,AD=DC=CB=1,∠BCD=120°,∴AB=2.
∴BD2=AB2+AD2-2AB•AD•cos60°=3.…(2分)
∴AB2=AD2+BD2,∴AD⊥BD.
∵平面BFED⊥平面ABCD,平面BFED∩平面ABCD=BD,DE?平面BEFD,DE⊥DB,
∴DE⊥平面ABCD,…(4分)
∴DE⊥AD,又DE∩BD=D,∴AD⊥平面BFED.…(6分)
(Ⅱ)由(Ⅰ)可建立分别以直线DA,DB,DE为x轴,y轴,z轴的,如图所示的空间直角坐标系,
令EP=λ (0≤λ≤$\sqrt{3}$),则D(0,0,0),A(1,0,0),$B({0,\sqrt{3},0})$,P(0,λ,1),
∴$\overrightarrow{AB}=(-1,\sqrt{3},0)$,$\overrightarrow{BP}=(0,λ-\sqrt{3},1)$,…(8分)设$\overrightarrow{n_1}=(x,y,z)$为平面PAB的一个法向量,
由$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{AB}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{BP}=0}\end{array}\right.$,得$\left\{\begin{array}{l}-x+\sqrt{3}y=0\\(λ-\sqrt{3})y+z=0\end{array}\right.$,取y=1,则$\overrightarrow{n_1}=(\sqrt{3},1,\sqrt{3}-λ)$,
…(10分)
∵$\overrightarrow{n_2}=({0,1,0})$是平面ADE的一个法向量,
∴$cosθ=\frac{{\left|{\overrightarrow{n_1}•\overrightarrow{n_2}}\right|}}{{\left|{\overrightarrow{n_1}}\right|\left|{\overrightarrow{n_2}}\right|}}=\frac{1}{{\sqrt{3+1+{{({\sqrt{3}-λ})}^2}}×1}}=\frac{1}{{\sqrt{{{({λ-\sqrt{3}})}^2}+4}}}$.
∵0≤λ≤$\sqrt{3}$,∴当λ=$\sqrt{3}$时,cosθ有最大值$\frac{1}{2}$.
∴θ的最小值为$\frac{π}{3}$.…(12分)
点评 本题考查线面垂直的证明,考查角的最小值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{e}$-2 | B. | 1-2e | C. | 1-e | D. | 2-$\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
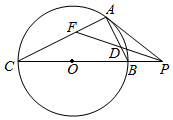 如图,点A在⊙O上,过点O的割线PBC交⊙O于点B,C,且PA=4,PB=2,OB=3,∠APC的平分线分别交AB,AC于D,E.
如图,点A在⊙O上,过点O的割线PBC交⊙O于点B,C,且PA=4,PB=2,OB=3,∠APC的平分线分别交AB,AC于D,E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 1 | C. | $\frac{\sqrt{3}}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
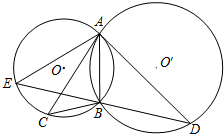 如图,⊙O和⊙O′相交于A,B两点,过A作两圆的切线分别交两圆于C,D两点,连结DB并延长交⊙O于点E,已知AC=BD=3.
如图,⊙O和⊙O′相交于A,B两点,过A作两圆的切线分别交两圆于C,D两点,连结DB并延长交⊙O于点E,已知AC=BD=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,$\frac{7}{6}π}$) | B. | (2,-$\frac{7}{6}π}$) | C. | (-2,-$\frac{11π}{6}}$) | D. | (-2,$\frac{13}{6}π}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com