
分析 令g(x)=exf(x)-ex-1,利用导数可判断函数g(x)的单调性,由已知条件可得函数g(x)的零点,由此可解得不等式.
解答 解:令g(x)=exf(x)-ex-1,则g′(x)=exf(x)+exf′(x)-ex=ex[f(x)+f′(x)-1],
∵f(x)+f′(x)>1,
∴f(x)+f′(x)-1>0,
∴g′(x)>0,即g(x)在R上单调递增,
又f(0)=2,∴g(0)=e0f(0)-e0-1=2-1-1=0,
故当x>0时,g(x)>g(0),即exf(x)-ex-1>0,整理得exf(x)>ex+1,
∴exf(x)>ex+1的解集为(0,+∞).
故答案为:(0,+∞)
点评 本题考查函数单调性的性质及其应用,考查抽象不等式的求解,考查导数与函数单调性的关系,综合性较强,属于中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 使用年数 | 2 | 4 | 6 | 8 | 10 |
| 售价 | 16 | 13 | 9.5 | 7 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
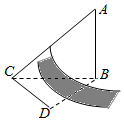 如图,测量河对岸的旗杆AB高时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=a,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )
如图,测量河对岸的旗杆AB高时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=a,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )| A. | $\frac{{\sqrt{2}}}{2}a$ | B. | $\frac{{3\sqrt{2}}}{2}a$ | C. | $\frac{{\sqrt{3}}}{2}a$ | D. | $\frac{{\sqrt{6}}}{2}a$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21 | B. | 20 | C. | 19 | D. | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
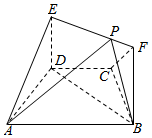 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com