
【题目】已知:函数f(x)= ![]() (a>0且a≠1).
(a>0且a≠1).
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判断函数f(x)的奇偶性,并加以证明;
(Ⅲ)设a=![]() ,解不等式f(x)>0.
,解不等式f(x)>0.
【答案】(1) (-1,1);(2)见解析;(3) {x|-1<x<0}
【解析】试题分析:(I)根据对数函数有意义可知真数要大于0,列不等式组,解之即可求出函数的定义域;(Ⅱ)根据函数的奇偶性的定义进行判定,计箄![]() 与
与![]() 的关系,从而确定函数的奇偶性;(Ⅲ)将
的关系,从而确定函数的奇偶性;(Ⅲ)将![]() 代入,根据函数的定义域和函数的单调性列不等式组,解之即可求出
代入,根据函数的定义域和函数的单调性列不等式组,解之即可求出![]() 的范围.
的范围.
试题解析:(Ⅰ)由题知: ![]() ,解得:-1<x<1,所以函数f(x)的定义域为(-1,1);
,解得:-1<x<1,所以函数f(x)的定义域为(-1,1);
(Ⅱ)奇函数,
证明:因为函数f(x)的定义域为(-1,1),所以对任意x∈(-1,1),
f(-x)= ![]() =
=![]() =-f(x)
=-f(x)
所以函数f(x)是奇函数;
(Ⅲ)由题知: ![]() 即有
即有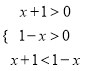 ,解得:-1<x<0,
,解得:-1<x<0,
所以不等式f(x)>0的解集为{x|-1<x<0}.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线C的参数方程: ![]() ,直线l的参数方程为
,直线l的参数方程为 ![]() .
.
(1)若直线l与曲线C只有一个公共点,求实数a;
(2)若点P,Q分别为直线l与曲线C上的动点,若 ![]() ,求实数a.
,求实数a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是四棱锥的平面展开图,其中四边形ABCD为正方形,E,F,G,H分别为PA,PD,PC,PB的中点,在此几何体中,给出下面四个结论中错误的是( )

A. 平面![]() 平面ABCD
平面ABCD
B. 直线BE,CF相交于一点
C. EF//平面BGD
D. ![]() 平面BGD
平面BGD
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量 ![]() =(a,
=(a, ![]() b)与
b)与 ![]() =(cosA,sinB)平行. (Ⅰ)求A;
=(cosA,sinB)平行. (Ⅰ)求A;
(Ⅱ)若a= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com