
分析 将三角形放入坐标系中,求出对应点的坐标,利用向量数量积的坐标进行转化为一元二次函数进行求解.
解答 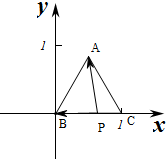 解:将三角形放入坐标系中,则B(0,0),C(1,0),A($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
解:将三角形放入坐标系中,则B(0,0),C(1,0),A($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
∵P为边BC上一动点,
∴设P(x,0),则0≤x≤1,
则$\overrightarrow{PA}$•$\overrightarrow{PB}$=($\frac{1}{2}$-x,$\frac{\sqrt{3}}{2}$)•(-x,0)=x2-$\frac{1}{2}$x=(x-$\frac{1}{4}$)2$-\frac{1}{16}$,
∴当x=$\frac{1}{4}$时,$\overrightarrow{PA}$•$\overrightarrow{PB}$取得最小值$-\frac{1}{16}$,
故答案为:$-\frac{1}{16}$.
点评 本题主要考查平面向量数量积的应用,利用坐标法建立坐标系转化为一元二次函数是解决本题的关键.


科目:高中数学 来源:2017届湖北省百所重点校高三联合考试数学(理)试卷(解析版) 题型:选择题
为得到函数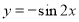 的图象,可将函数
的图象,可将函数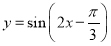 的图象( )
的图象( )
A.向左平移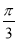 个单位 B.向左平移
个单位 B.向左平移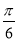 个单位
个单位
C.向右平移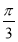 个单位 D.向右平移
个单位 D.向右平移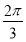 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患有颈椎疾病 | 没有患颈椎疾病 | 合计 | |
| 白领 | 5 | ||
| 蓝领 | 10 | ||
| 合计 | 50 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com