
分析 (1)求出导数,切线的斜率,由点斜式方程,即可得到切线方程;
(2)求出a=-1的函数的导数,求出单调区间和极值,以及端点的函数值,即可得到最值.
解答 解:(1)当a=0时,f(x)=$\frac{1}{3}$x3+x2+1,
∴f(3)=19,∵f′(x)=x2+2x,
曲线在点(3,19)处的切线的斜率k=f′(3)=15
∴所求的切线方程为y-19=15(x-3),即y=15x-26,
(2)当a=-1时,函数f(x)=$\frac{1}{3}$x3-x2-3x+1,
∵f′(x)=x2-2x-3,令f′(x)=0得x1=-1,x2=3,
x2∉[0,4],当x∈(0,3)时,f'(x)<0,
即函数y=f(x)在(0,3)上单调递减,
当x∈(3,4)时,f′(x)>0,即函数y=f(x)在(3,4)上单调递增,
∴函数y=f(x)在[0,4]上有最小值,f(x)最小值=f(3)=-8,
又f(0)=1,f(4)=-$\frac{17}{3}$;
∴当a=-1时,函数y=f(x)在[0,4]上的最大值和最小值分别为1,-8.
点评 本题考查导数的运用:求切线方程和求单调区间、求极值和最值,考查运算能力,属于中档题.


科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:解答题
已知动圆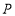 (
(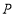 为圆心)经过点
为圆心)经过点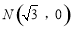 ,并且与圆
,并且与圆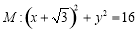 相切.
相切.
(Ⅰ)求点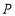 的轨迹
的轨迹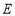 的方程;
的方程;
(Ⅱ)经过点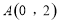 的直线
的直线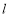 与曲线
与曲线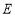 相交于点
相交于点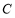 ,
,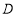 ,并且
,并且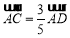 ,求直线
,求直线 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com