练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．一个三棱锥的三视图如图所示，则该三棱锥的外接球的表面积为29π．

    分析 该三棱锥为长方体切去四个小三棱锥得到的，故长方体的体对角线等于外接球的直径．

    解答 解：由三视图可知该三棱锥为边长为2，3，4的长方体切去四个小棱锥得到的几何体．
    设该三棱锥的外接球半径为R，
    ∴2R=$\sqrt{4+9+16}$=$\sqrt{29}$，
    ∴R=$\frac{\sqrt{29}}{2}$．
    ∴外接球的表面积为S=4πR2=29π．
    故答案为：29π．

    点评 本题考查了常见几何体与外接球的关系，根据三视图得出三棱锥与长方体的关系是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届湖北省百所重点校高三联合考试数学（理）试卷（解析版） 题型：解答题

    已知函数．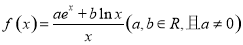

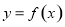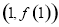    （1）若曲线在点处的切线与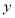轴垂直，且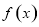有极大值，求实数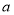的取值范围；

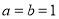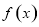    （2）若，试判断在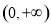上的单调性，并加以证明．（提示：）．

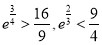    查看答案和解析>>

    科目：高中数学 来源：2017届河北沧州市高三9月联考数学（文）试卷（解析版） 题型：选择题

    正方体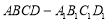的顶点都在同一球面上，且此球体积为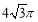，则正方体的体积为（ ）

    A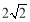． B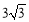． C．8 D．27

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．为了了解某工业园中员工的颈椎疾病与工作性质是否有关，在工业园内随机的对其中50名工作人员是否患有颈椎疾病进行了抽样调查，得到如下的列联表．
    患有颈椎疾病没有患颈椎疾病合计
    白领5
    蓝领10
    合计50
    已知在全部50人中随机抽取1人，抽到患有颈椎疾病的人的概率为$\frac{3}{5}$．
    （1）请将上面的列联表补充完整，并判断是否有99.5%的把握认为患颈椎疾病与工作性质有关？说明你的理由；
    （2）已知在患有颈椎疾病的10名蓝领中，有3位工龄在15年以上，现在从患有颈椎疾病的10名蓝领中，选出3人进行工龄的调查，记选出工龄在15年以上的人数为ξ，求ξ的分布列及数学期望．
    参考公式：${k^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
    下面的临界值表仅供参考：
    P（K2≥k0）0.150.100.050.0250.0100.0050.001
    k02.0722.7063.8415.0246.6357.87910.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知数列{an}满足：${a_1}∈{N^+}，{a_1}≤36$，且${a_{n+1}}=\left\{\begin{array}{l}2{a_n}，{a_n}≤18\\ 2{a_n}-36，{a_n}＞18\end{array}\right.（{n=1，2，…}）$，记集合$M=\left\{{{a_n}|n∈{N^+}}\right\}$
    （1）若a1=6，写出集合M的所有元素；
    （2）求集合M的元素个数的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．△ABC中，A＞B是tanA＞tanB的（　　）
    A．充要条件B．充分不必要条件
    C．必要不充分条件D．既不必要又不充分条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=$\frac{1}{3}$x3+（2a+1）x2+3a（a+2）x+1，a∈R．
    （1）当a=0时，求曲线y=f（x）在点（3，f（3））处的切线方程；
    （2）当a=-1时，求函数y=f（x）在[0，4]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．（1）化简：$tanα+\sqrt{\frac{1}{{{{cos}^2}α}}-1}+2{sin^2}α+2{cos^2}α$，其中α是第四象限角
    （2）化简：$\frac{sin（α+π）tan（π-α）cos（2π-α）}{{sin（π-α）sin（\frac{π}{2}+α）}}+cos\frac{5π}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．极坐标方程ρ=2$\sqrt{2}$cos（$\frac{π}{4}-θ}$）表示图形的面积是2π．

    查看答案和解析>>

    同步练习册答案