练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．（1）计算$\frac{2{A}_{8}^{5}+7{A}_{8}^{4}}{{A}_{8}^{8}-{A}_{9}^{5}}$     
    （2）计算：C${\;}_{200}^{198}$+C${\;}_{200}^{196}$+2C${\;}_{200}^{197}$．

    分析 （1）利用排列数的计算公式即可得出．
    （2）利用组合数的计算公式即可得出．

    解答 解：（1）$\frac{2{A}_{8}^{5}+7{A}_{8}^{4}}{{A}_{8}^{8}-{A}_{9}^{5}}$=$\frac{2×8×7×6×5×4+7×8×7×6×5}{8×7×…×2×1-9×8×7×6×5}$=$\frac{2×4-7}{4×3×2×1-9}$=$\frac{1}{15}$．
    （2）C${\;}_{200}^{198}$+C${\;}_{200}^{196}$+2C${\;}_{200}^{197}$=${∁}_{201}^{197}$+${∁}_{201}^{198}$=${∁}_{201}^{198}$=${∁}_{202}^{4}$．

    点评 本题考查了排列数的计算公式、组合数的计算公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届河北沧州市高三9月联考数学（文）试卷（解析版） 题型：选择题

    正方体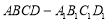的顶点都在同一球面上，且此球体积为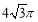，则正方体的体积为（ ）

    A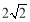． B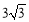． C．8 D．27

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=$\frac{1}{3}$x3+（2a+1）x2+3a（a+2）x+1，a∈R．
    （1）当a=0时，求曲线y=f（x）在点（3，f（3））处的切线方程；
    （2）当a=-1时，求函数y=f（x）在[0，4]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．（1）化简：$tanα+\sqrt{\frac{1}{{{{cos}^2}α}}-1}+2{sin^2}α+2{cos^2}α$，其中α是第四象限角
    （2）化简：$\frac{sin（α+π）tan（π-α）cos（2π-α）}{{sin（π-α）sin（\frac{π}{2}+α）}}+cos\frac{5π}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．双曲线$\frac{x^2}{2}$-y2=-1的焦点到其渐近线的距离等于（　　）
    A．$\frac{1}{2}$B．$\sqrt{2}$C．1D．$\frac{\sqrt{2}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．若，sinx-cosx＜0，则y=$\frac{sinx}{|sinx|}$+$\frac{cosx}{|cosx|}$+$\frac{tanx}{|tanx|}$函数的值域为{-1，3}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．计算cos$\frac{11π}{3}$+tan（-$\frac{3}{4}$π）=-$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．极坐标方程ρ=2$\sqrt{2}$cos（$\frac{π}{4}-θ}$）表示图形的面积是2π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．在△ABC中，已知下列条件解三角形：
    ①A=60°，a=$\sqrt{3}$，b=1；
    ②A=30°，a=1，b=2；
    ③A=30°，c=10，a=6；
    ④A=30°，c=10，a=5，
    其中有唯一解的序号为（　　）
    A．①②③B．①②④C．②③④D．①③④

    查看答案和解析>>

    同步练习册答案