练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知正四面体的棱长为， 为棱的中点，过作其外接球的截面，则截面面积的最小值为__________．

    【答案】

    【解析】将四面体放置于正方体中，可得正方体的外接球就是四面体的外接球，∵正四面体的棱长为，∴正方体的棱长为，可得外接球半径满足，解得， 为棱的中点，过作其外接球的截面，当截面到球心的距离最大时，截面圆的面积达最小值，此时球心到截面的距离等于正方体棱长的一半，可得截面圆的半径为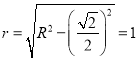，得到截面圆的面积最小值为．

    点睛:空间几何体与球接、切问题的求解方法

    (1)求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．

    (2)若球面上四点构成的三条线段两两互相垂直，且，一般把有关元素“补形”成为一个球内接长方体，利用求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A，B，C的对边分别为a，b，c，且(2b－c)cos A＝acos C．

    (1)求角A的大小；

    (2)若a＝3，b＝2c，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： （）的离心率为，以椭圆的四个顶点为顶点的四边形的面积为8.

    （Ⅰ）求椭圆的方程；

    （Ⅱ）如图，斜率为的直线与椭圆交于， 两点，点在直线的左上方.若，且直线， 分别与轴交于， 点，求线段的长度.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图, 在△中, 点在边上, .

    （Ⅰ）求；

    （Ⅱ）若△的面积是, 求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，且过点．

    （Ⅰ）求椭圆的方程．

    （Ⅱ）若， 是椭圆上两个不同的动点，且使的角平分线垂直于轴，试判断直线的斜率是否为定值？若是，求出该值；若不是，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳健型产品的收益与投资额成正比，投资股票等风险型产品的收益与投资额的算术平方根成正比．已知投资1万元时两类产品的收益分别为0.125万元和0.5万元（如图）．

    （1）分别写出两种产品的收益与投资额的函数关系式；
    （2）该家庭现有20万元资金，全部用于理财投资，问：怎么分配资金能使投资获得最大收益，其最大收益是多少万元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=lg（1+x）+lg（1﹣x）．
    （1）求函数f（x）的定义域；
    （2）判断函数f（x）的奇偶性；
    （3）求函数f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（ ）x ， 函数g（x）=log x．
    （1）若g（ax2+2x+1）的定义域为R，求实数a的取值范围；
    （2）当x∈[（ ）t+1 ， （ ）t]时，求函数y=[g（x）]2﹣2g（x）+2的最小值h（t）；
    （3）是否存在非负实数m，n，使得函数y=log f（x2）的定义域为[m，n]，值域为[2m，2n]，若存在，求出m，n的值；若不存在，则说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】据市场分析，某蔬菜加工点，当月产量在10吨至25吨时，月生产总成本（万元）可以看成月产量（吨）的二次函数．当月产量为10吨时，月总成本为20万元；当月产量为15吨时，月总成本最低为17.5万元．

    （1）写出月总成本（万元）关于月产量（吨）的函数关系；

    （2）已知该产品的销售价为每吨1.6万元，那么月产量为多少时，可获最大利润．

    （3）当月产量为多少吨时，每吨平均成本最低，最低成本是多少万元？

    查看答案和解析>>

    同步练习册答案