【题目】在△ABC中，内角A，B，C的对边分别为a，b，c，且(2b－c)cos A＝acos C．
(1)求角A的大小；
(2)若a＝3，b＝2c，求△ABC的面积．
【答案】（1）
（2）
【解析】试题分析：（1）根据已知，利用正弦定理，求出
，求出角A的大小；（2）由余弦定理的推论，求出边长c，由b=2c 求出边长b，由三角形面积公式求出面积。
试题解析： (1)根据正弦定理，由(2b－c)cos A＝acos C，
得2sin Bcos A＝sin Acos C＋sin Ccos A，
即2sin Bcos A＝sin(A＋C)，
所以2sin Bcos A＝sin B，
因为0<B<π，所以sin B≠0，
所以cos A＝
，因为0<A<π，所以A＝
.
(2)因为a＝3，b＝2c，由(1)得A＝，
所以cos A＝
＝
＝，
解得c＝
，所以b＝2.
所以S△ABC＝bcsin A＝×2××
＝
.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x2﹣2|x|﹣1．
（1）证明函数f（x）是偶函数；
（2）在如图所示的平面直角坐标系中作出函数f（x）的图象．并根据图象写出函数f（x）的单调区间； 
（3）求函数f（x）当x∈[﹣2，4]时的最大值与最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，平面ABDE⊥平面ABC，△ABC是等腰直角三角形，AC＝BC＝4，四边形ABDE是直角梯形，BD∥AE，BD⊥BA，BD＝
AE＝2，O，M分别为CE，AB的中点．
(1)求证：OD∥平面ABC；
(2)求直线CD和平面ODM所成角的正弦值；
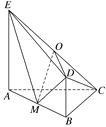
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
.
（1）若
是函数
的极值点，1为函数
的一个零点，求函数
在
上的最小值.
（2）当
时，函数
与
轴在
内有两个不同的交点，求
的取值范围.（其中
是自然对数的底数）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝
，数列{an}满足a1＝1，an＋1＝f(an)(n∈N*)．
(1)证明数列{
}是等差数列，并求出数列{an}的通项公式；
(2)记Sn＝a1a2＋a2a3＋…＋anan＋1，求Sn．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x+ 
，且f（1）=2．
（1）求m的值；
（2）判断f（x）的奇偶性；
（3）用定义法证明f（x）在区间（1，+∞）上是增函数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
