
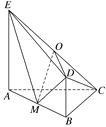
【题目】如图所示,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=![]() AE=2,O,M分别为CE,AB的中点.
AE=2,O,M分别为CE,AB的中点.
(1)求证:OD∥平面ABC;
(2)求直线CD和平面ODM所成角的正弦值;
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)通过证明线线平行得到线面平行;(2)C为原点,分别以CA,CB所在直线为x,y轴,以过点C且与平面ABC垂直的直线为z轴,建立空间直角坐标系,求出平面ODM的一个法向量,利用直线与平面所成的角的公式,求出直线CD和平面ODM所成角的正弦值。
试题解析:(1)证明 如图,取AC中点F,连接OF,FB.
∵F是AC中点,O为CE中点,
∴OF∥EA且OF=![]() EA.
EA.
又BD∥AE且BD=![]() AE,
AE,
∴OF∥DB且OF=DB,
∴四边形BDOF是平行四边形,∴OD∥FB.
又∵FB平面ABC,OD平面ABC,
∴OD∥平面ABC.
(2)解 ∵平面ABDE⊥平面ABC,平面ABDE∩平面ABC=AB,DB平面ABDE,且BD⊥BA,
∴DB⊥平面ABC.
∵BD∥AE,∴EA⊥平面ABC.
又△ABC是等腰直角三角形,且AC=BC,
∴∠ACB=90°,
∴以C为原点,分别以CA,CB所在直线为x,y轴,以过点C且与平面ABC垂直的直线为z轴,建立空间直角坐标系,如图所示.
∵AC=BC=4,∴C(0,0,0),A(4,0,0),B(0,4,0),D(0,4,2),E(4,0,4),O(2,0,2),M(2,2,0),
∴![]() =(0,4,2),
=(0,4,2),![]() =(-2,4,0),
=(-2,4,0),![]() =(-2,2,2).
=(-2,2,2).
设平面ODM的法向量为n=(x,y,z),
则由n⊥![]() ,n⊥
,n⊥![]() ,可得
,可得![]()
令x=2,得y=1,z=1,∴n=(2,1,1).
设直线CD和平面ODM所成角为θ,
则sin θ=![]() =
=![]() =
=![]() =
=![]() .
.
∴直线CD和平面ODM所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知下图中,四边形 ABCD是等腰梯形, ![]() ,
, ![]() ,O、Q分别为线段AB、CD的中点,OQ与EF的交点为P,OP=1,PQ=2,现将梯形ABCD沿EF折起,使得
,O、Q分别为线段AB、CD的中点,OQ与EF的交点为P,OP=1,PQ=2,现将梯形ABCD沿EF折起,使得![]() ,连结AD、BC,得一几何体如图所示.
,连结AD、BC,得一几何体如图所示.
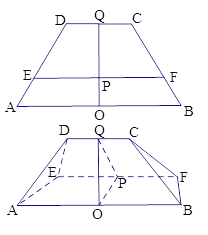
(Ⅰ)证明:平面ABCD![]() 平面ABFE;
平面ABFE;
(Ⅱ)若上图中, ![]() ,CD=2,求平面ADE与平面BCF所成锐二面角的余弦值.
,CD=2,求平面ADE与平面BCF所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=lgx+1(1≤x≤100),则g(x)=f2(x)+f(x2)的值域为( )
A.[﹣2,7]
B.[2,7]
C.[﹣2,14]
D.[2,14]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域是(0,+∞),且满足f(xy)=f(x)+f(y),当x>1时,有f(x)>0.
(1)求f(1),判定并证明f(x)的单调性;
(2)若f(2)=1,解不等式f(﹣x)+f(3﹣x)≥﹣2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且(2b-c)cos A=acos C.
(1)求角A的大小;
(2)若a=3,b=2c,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+1,a,b∈R,当x=﹣1时,函数f(x)取到最小值,且最小值为0;
(1)求f(x)解析式;
(2)关于x的方程f(x)=|x+1|﹣k+3恰有两个不相等的实数解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为15°,边界忽略不计) 即为中奖.

乙商场:从装有3个白球3个红球的盒子中一次性摸出2个球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖.
问:购买该商品的顾客在哪家商场中奖的可能性大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是椭圆
是椭圆![]() 上两个不同的动点,且使
上两个不同的动点,且使![]() 的角平分线垂直于
的角平分线垂直于![]() 轴,试判断直线
轴,试判断直线![]() 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com