
【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为15°,边界忽略不计) 即为中奖.

乙商场:从装有3个白球3个红球的盒子中一次性摸出2个球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖.
问:购买该商品的顾客在哪家商场中奖的可能性大?
【答案】在乙商场中奖的可能性大
【解析】试题分析:根据题意可知需分别求出在两个商场中奖的概率,然后比较中奖概率的大小即可知道结论.显然甲商场属于几何概型,需要求得阴影部分的面积占整个圆形面积的概率即为甲商场中奖的概率;乙商场中奖的概率根据古典概型,列出所有的基本事件数,进而得到中奖的事件数,进而求得乙商场中奖的概率,进而比较得到乙商场中奖的可能性大的结论.
试题解析:设顾客去甲商场,转动圆盘,指针指向阴影部分为事件![]() ,
,
试验的全部结果构成的区域为圆盘,面积为![]() (
(![]() 为圆盘的半径),阴影区域的面积为
为圆盘的半径),阴影区域的面积为![]() .
.
所以, 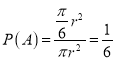 .
.
设顾客去乙商场一次摸出两个红球为事件![]() ,记盒子中
,记盒子中![]() 个白球为
个白球为![]() ,
, ![]() ,
, ![]() ,
, ![]() 个红球为
个红球为![]() ,
, ![]() ,
, ![]() ,记
,记![]() 为一次摸球的结果,则一切可能的结果有:
为一次摸球的结果,则一切可能的结果有: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共
,共![]() 种.
种.
摸到的![]() 个球都是红球有
个球都是红球有![]() ,
, ![]() ,
, ![]() ,共
,共![]() 种.
种.
所以, ![]()
![]() .
.
因为![]() ,
,
所以,顾客在乙商场中奖的可能性大.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,左顶点为
,左顶点为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条相互垂直的直线分别与椭圆
作两条相互垂直的直线分别与椭圆![]() 交于(不同于点
交于(不同于点![]() 的)
的)![]() 两点.试判断直线
两点.试判断直线![]() 与
与![]() 轴的交点是否为定点,若是,求出定点坐标;若不是,请说明理由.
轴的交点是否为定点,若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
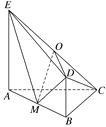
【题目】如图所示,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=![]() AE=2,O,M分别为CE,AB的中点.
AE=2,O,M分别为CE,AB的中点.
(1)求证:OD∥平面ABC;
(2)求直线CD和平面ODM所成角的正弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,数列{an}满足a1=1,an+1=f(an)(n∈N*).
,数列{an}满足a1=1,an+1=f(an)(n∈N*).
(1)证明数列{![]() }是等差数列,并求出数列{an}的通项公式;
}是等差数列,并求出数列{an}的通项公式;
(2)记Sn=a1a2+a2a3+…+anan+1,求Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列给出四组函数,表示同一函数的是( )
A.f(x)=x﹣1,g(x)= ![]() ﹣1
﹣1
B.f(x)=2x+1,g(x)=2x﹣1
C.f(x)=|x|,g(x)= ![]()
D.f(x)=1,g(x)=x0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() ,且f(1)=2.
,且f(1)=2.
(1)求m的值;
(2)判断f(x)的奇偶性;
(3)用定义法证明f(x)在区间(1,+∞)上是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】河南多地遭遇跨年霾,很多学校调整元旦放假时间,提前放假让学生们在家里躲霾,郑州市根据《郑州市人民政府办公厅关于将重污染天气黄色预警升级为红色预警的通知》.自12月29日12时将黄色预警升级为红色预警,12月30日0时启动I级响应,明确要求:“幼儿园、中小学等教育机构停课,停课不停学”,学生和家长对停课这一举措褒贬不一,有为了健康赞成的,有怕耽误学习不赞成的.某调查机构为了了解公众对该举措的态度,随机调查采访了50人,将调查情况整理汇总成下表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(1)请补全被调查人员年龄的频率分布直方图;
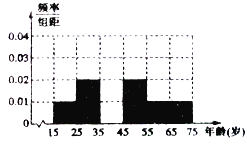
(2)若从年龄在![]() 的被调查者中分别随机选取一人进行追踪调查,求这两人都赞成“停课”这一举措的概率.
的被调查者中分别随机选取一人进行追踪调查,求这两人都赞成“停课”这一举措的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某蔬菜商店买进的土豆![]() (吨)与出售天数
(吨)与出售天数![]() (天)之间的关系如表所示:
(天)之间的关系如表所示:
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
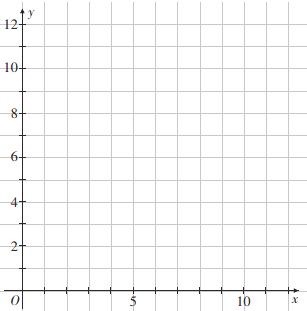
(Ⅰ)请根据表中数据在所给网格中绘制散点图;
(Ⅱ)请根据表中提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (其中
(其中![]() 保留2位有效数字);
保留2位有效数字);
(Ⅲ)根据(Ⅱ)中的计算结果,若该蔬菜商店买进土豆40吨,则预计可以销售多少天(计算结果保留整数)?
附: 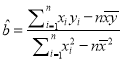 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com