练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列给出四组函数，表示同一函数的是（ ）
    A.f（x）=x﹣1，g（x）= ﹣1
    B.f（x）=2x+1，g（x）=2x﹣1
    C.f（x）=|x|，g（x）=
    D.f（x）=1，g（x）=x0

    【答案】C
    【解析】解：对于A：f（x）=x﹣1，其定义域为R，而g（x）= ﹣1的定义域为{x|x≠0}，定义域不同，∴不是同一函数；
    对于B：f（x）=2x+1，g（x）=2x﹣1它们的定义域为R，但对应关系不相同，∴不是同一函数；
    对于C：f（x）=|x|，其定义域为R，g（x）= =|x|的定义域为R，它们的定义域相同，对应关系也相同，∴是同一函数；
    对于D：f（x）=1其定义域为R，而g（x）=x0的定义域为{x|x≠0}，定义域不同，∴不是同一函数；
    故选C．
    根据两个函数的定义域相同，对应关系也相同，判断它们是同一函数即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某家具厂有方木料，五合板，准备加工成书桌和书橱出售.已知生产每张书桌需要方木料、五合板；生产每个书橱需要方木枓、五合板.出售一张书桌可获利润元，出售一个书橱可获利润元，怎样安排生产可使所得利润最大？最大利润为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）的定义域是（0，+∞），且满足f（xy）=f（x）+f（y），当x＞1时，有f（x）＞0．
    （1）求f（1），判定并证明f（x）的单调性；
    （2）若f（2）=1，解不等式f（﹣x）+f（3﹣x）≥﹣2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数f（x）=ax2+bx+1，a，b∈R，当x=﹣1时，函数f（x）取到最小值，且最小值为0；
    （1）求f（x）解析式；
    （2）关于x的方程f（x）=|x+1|﹣k+3恰有两个不相等的实数解，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】运货卡车以每小时x千米的速度匀速行驶130千米，按交通法规限制50≤x≤100（单位：千米/时）．假设汽油的价格是每升2元，而汽车每小时耗油升，司机的工资是每小时14元．

    （1）求这次行车总费用y关于x的表达式；

    （2）当x为何值时，这次行车的总费用最低，并求出最低费用的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两家商场对同一种商品开展促销活动，对购买该商品的顾客两家商场的奖励方案如下：

    甲商场：顾客转动如图所示圆盘，当指针指向阴影部分(图中四个阴影部分均为扇形，且每个扇形圆心角均为15°，边界忽略不计) 即为中奖.

    乙商场：从装有3个白球3个红球的盒子中一次性摸出2个球(球除颜色外不加区分)，如果摸到的是2个红球，即为中奖.

    问：购买该商品的顾客在哪家商场中奖的可能性大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图如下图，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为a，视力在4.6到5.0之间的学生数为b，则a，b的值分别为 (　 　)

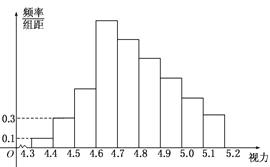
    A. 0.27,78 B. 0.27,83 C. 2.7,78 D. 2.7,83

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是公差不为零的等差数列，，且，，成等比数列．

    （1）求数列的通项；

    （2）求数列的前项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果定义在（﹣∞，0）∪（0，+∞）上的奇函数f（x），在（0，+∞）内是减函数，又有f（3）=0，则xf（x）＜0的解集为（ ）
    A.{x|﹣3＜x＜0或x＞3}
    B.{x|x＜﹣3或0＜x＜3}
    C.{x|﹣3＜x＜0或0＜x＜3}
    D.{x|x＜﹣3或x＞3}

    查看答案和解析>>

    同步练习册答案