
| C | 2 2 |
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
| C | 2 2 |
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |


科目:高中数学 来源: 题型:
A、已知函数f(x)=
| ||
B、设回归直线方程为
| ||
| C、已知ξ服从正态分布 N(0,σ2),且P(-2≤ξ≤0)=0.4,则P(ξ>2)=0.1 | ||
| D、对于命题p:“?x∈R,x2+x+1<0”,则?p:“?x∈R,x2+x+1>0” |
查看答案和解析>>
科目:高中数学 来源: 题型:
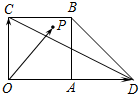 如图,四边形OABC是边长为1的正方形,点D在OA的延长线上,且OD=2,点P为△BCD内(含边界)的动点,设
如图,四边形OABC是边长为1的正方形,点D在OA的延长线上,且OD=2,点P为△BCD内(含边界)的动点,设| OP |
| OC |
| OD |
查看答案和解析>>
科目:高中数学 来源: 题型:
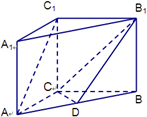 如图,在直三棱柱ABC-A1B1C1(侧棱与底面垂直的棱柱称为直棱柱)中,AC=CC1=3,BC=4,AB=5,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1(侧棱与底面垂直的棱柱称为直棱柱)中,AC=CC1=3,BC=4,AB=5,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
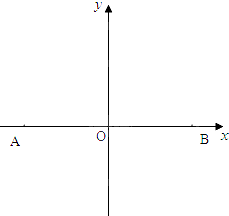 如图,A,B两地相距10km,A(-5,0),B(5,0).有一种商品,A、B两地均有出售且价格相同,某地居民从两地之一购得商品运回来,每公里的运费A地是B地的3倍.问该地居民应如何选择A地或B地购买此种商品最合算?(仅从运费的多少来考虑)
如图,A,B两地相距10km,A(-5,0),B(5,0).有一种商品,A、B两地均有出售且价格相同,某地居民从两地之一购得商品运回来,每公里的运费A地是B地的3倍.问该地居民应如何选择A地或B地购买此种商品最合算?(仅从运费的多少来考虑)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com