
【题目】已知两点A(﹣1,2),B(m,3).且实数m∈[﹣ ![]() ﹣1,
﹣1, ![]() ﹣1],求直线AB的倾斜角α的取值范围.
﹣1],求直线AB的倾斜角α的取值范围.
科目:高中数学 来源: 题型:
【题目】某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).
(1)写出楼房平均综合费用y关于建造层数x的函数关系式;
(2)该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面α过正方体ABCD﹣A1B1C1D1的顶点A,α∥平面CB1D1 , α∩平面ABCD=m,α∩平面AB B1A1=n,则m,n所成角的正弦值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,曲线![]() 的普通方程为
的普通方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)求曲线![]() 与
与![]() 焦点的极坐标
焦点的极坐标![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0, ![]() ),以A,B为焦点且过点D的双曲线的离心率为e1 , 以C,D为焦点且过点A的椭圆的离心率为e2 , 则( )
),以A,B为焦点且过点D的双曲线的离心率为e1 , 以C,D为焦点且过点A的椭圆的离心率为e2 , 则( ) 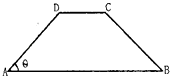
A.随着角度θ的增大,e1增大,e1e2为定值
B.随着角度θ的增大,e1减小,e1e2为定值
C.随着角度θ的增大,e1增大,e1e2也增大
D.随着角度θ的增大,e1减小,e1e2也减小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+y2=9内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(1)当l经过圆心C时,求直线l的方程; (写一般式)
(2)当直线l的倾斜角为45°时,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且a≠1,函数f(x)= ![]() (a﹣x﹣ax),g(x)=﹣ax+2.
(a﹣x﹣ax),g(x)=﹣ax+2.
(1)指出f(x)的单调性(不要求证明);
(2)若有g(2)+f(2)=3,求g(﹣2)+f(﹣2)的值;
(3)若h(x)=f(x)+g(x)﹣2,求使不等式h(x2+tx)+h(4﹣x)<0恒成立的t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com