
分析 (1)讨论对称轴与区间[0,2]的关系,判断f(x)的单调性,列出方程组解出a,b;
(2)令g(x)=$\frac{f(x)}{x}$,讨论极值点与区间[1,2]的关系判断g(x)的单调性,列出不等式组解出b.
解答 (1)抛物线的对称轴为$x=-\frac{b}{2a}$,
①当$-\frac{b}{2a}<2$时,即b>-4a时,
当$x=-\frac{b}{2a}$时,$f{(x)_{max}}=f(-\frac{b}{2a})=a×\frac{b^2}{{4{a^2}}}-\frac{b^2}{2a}+c=\frac{{-{b^2}}}{4a}+c=\frac{9}{8}$,f(x)min=f(2)=4a+2b+c=-2,
∴$\left\{\begin{array}{l}-\frac{b^2}{4a}+c=\frac{9}{8}\\ 4a+2b=-2\end{array}\right.$,
∴a=-2,b=3.
②当$-\frac{b}{2a}≥2$时,即b≥-4a时,f(x)在[0,2]上为增函数,f(x)min=f(0)=0与f(x)min=-2矛盾,无解,
综合得:a=-2,b=3.
(2)$|\frac{f(x)}{x}|≤2$对任意x∈[1,2]恒成立,即$|ax+\frac{1}{x}+b|≤2$对任意x∈[1,2]恒成立,
即$-2≤ax+\frac{1}{x}+b≤2$对任意x∈[1,2]恒成立,
令$g(x)=ax+\frac{1}{x}+b$,则$\left\{\begin{array}{l}{[g(x)]_{max}}≤2\\{[g(x)]_{min}}≥-2\end{array}\right.$,
∵0<a<1,∴$\frac{1}{{\sqrt{a}}}>1$,
(ⅰ)若$\frac{1}{{\sqrt{a}}}≥2$,即$0<a≤\frac{1}{4}$时,g(x)在[1,2]单调递减,此时$\left\{\begin{array}{l}{[g(x)]_{max}}=g(1)≤2\\{[g(x)]_{min}}=g(2)≥-2\end{array}\right.$,
即$\left\{\begin{array}{l}a+1+b≤2\\ 2a+\frac{1}{2}+b≥-2\end{array}\right.$,得$\left\{\begin{array}{l}b≤1-a\\ b≥-2a-\frac{5}{2}\end{array}\right.$,此时$(-2a-\frac{5}{2})-(1-a)=-a-\frac{7}{2}<0$,∴$(-2a-\frac{5}{2})<(1-a)$
∴$-2a-\frac{5}{2}≤b≤1-a$.
(ⅱ)若$1<\frac{1}{{\sqrt{a}}}<2$,即$\frac{1}{4}<a<1$时,g(x)在$[1,\frac{1}{{\sqrt{a}}}]$单调递减,在$[\frac{1}{{\sqrt{a}}},2]$单调递增,
此时,${[g(x)]_{min}}=g(\frac{1}{{\sqrt{a}}})≥-2⇒2\sqrt{a}+b≥-2⇒b≥-2-2\sqrt{a}$,
只要$\left\{\begin{array}{l}g(1)=a+1+b≤2\\ g(2)=2a+\frac{1}{2}+b≤2\\ b≥-2\sqrt{a}-2\end{array}\right.$$⇒\left\{\begin{array}{l}b≤1-a\\ b≤\frac{3}{2}-2a\\ b≥-2\sqrt{a}-2\end{array}\right.$,$(1-a)-(\frac{3}{2}-2a)=a-\frac{1}{2}$
当$\frac{1}{2}≤a<1$时,$1-a≥\frac{3}{2}-2a$,$-2\sqrt{a}-2≤b≤\frac{3}{2}-2a$
当$\frac{1}{4}<a<\frac{1}{2}$时,$1-a<\frac{3}{2}-2a$,$-2\sqrt{a}-2≤b≤1-a$.
综上得:①$0<a≤\frac{1}{4}$时,$-2a-\frac{5}{2}≤b≤1-a$;
②$\frac{1}{4}<a<\frac{1}{2}$时,$-2\sqrt{a}-2≤b≤1-a$;
③$\frac{1}{2}≤a<1$时,$-2\sqrt{a}-2≤b≤\frac{3}{2}-2a$.
点评 本题考查了二次函数的单调性,最值,分类讨论思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
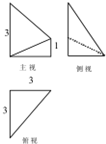
| A. | 18cm3 | B. | 6cm3 | C. | $\frac{9}{2}c{m^3}$ | D. | $\frac{27}{2}c{m^3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
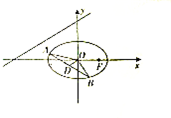 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,右焦点F到直线x=$\frac{a^2}{c}$的距离为1.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,右焦点F到直线x=$\frac{a^2}{c}$的距离为1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
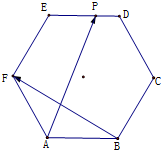 如图,正六边形ABCDEF的边长为2,P是线段DE上的任意一点,则$\overrightarrow{AP}$•$\overrightarrow{BF}$的取值范围为[0,6]..
如图,正六边形ABCDEF的边长为2,P是线段DE上的任意一点,则$\overrightarrow{AP}$•$\overrightarrow{BF}$的取值范围为[0,6]..查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,且AB=4,BC=CD=ED=EA=2.
如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,且AB=4,BC=CD=ED=EA=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com