
| A. | [-4,-2] | B. | [-2,6] | C. | [0,8] | D. | [2,4] |
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 空间中两条异面直线所成的角的范围是[0°,90°] | |
| B. | 平面直角坐标系中直线的倾斜角的范围是[0°,180°) | |
| C. | 二面角的平面角的范围是[0°,180°] | |
| D. | 直线与平面所成的角的范围是[0°,90°] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,1] | B. | [-2,2] | C. | [-2,3] | D. | [-2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:选择题
以下四个命题中:
①在回归分析中, 可用相关指数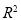 的值判断的拟合效果,
的值判断的拟合效果,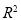 越大,模型的拟合效果越好;
越大,模型的拟合效果越好;
②两个随机变量的线性相关性越强,相关系数的绝对值越接近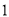 ;
;
③若数据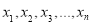 的方差为
的方差为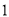 ,则
,则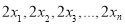 的方差为
的方差为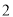 ;
;
④对分类变量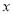 与
与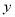 的随机变量
的随机变量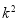 的观测值
的观测值 来说,
来说,  越小,判断“
越小,判断“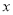 与
与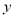 有关系”的把握程度越大.
有关系”的把握程度越大.
其中真命题的个数为( )
A.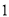 B.
B.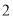 C.
C.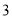 D.
D.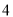
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com