
分析 (1)由题意根据正弦定理求得∴(2sinC-sinB)cosA=sinAcosB,由A=π-(B+C),根据诱导公式及两角和正弦公式,即可求得A的值;
(2)过D作DE∥AB于E,则△ADE中,ED=$\frac{1}{3}$AC=1,∠DEA=$\frac{2π}{3}$,由余弦定理可知△ABC为直角三角形,a=BC=3$\sqrt{3}$.
解答  解:(1)由$\frac{2c-b}{a}=\frac{cosB}{cosA}$,则(2c-b)cosA=acosB,
解:(1)由$\frac{2c-b}{a}=\frac{cosB}{cosA}$,则(2c-b)cosA=acosB,
由正弦定理可知:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R,则a=2RsinA,b=2RsinB,c=2RsinC,
∴(2sinC-sinB)cosA=sinAcosB,
整理得:2sinCcosA-sinBcosA=sinAcosB,
由A=π-(B+C),则sinA=sin[π-(B+C)]=sin(B+C),
即2sinCcosA=sin(A+B)=sinC,
由sinC≠0,则cosC=$\frac{1}{2}$,即A=$\frac{π}{3}$,
∴角A的大小$\frac{π}{3}$;
(2)过D作DE∥AB于E,则△ADE中,ED=$\frac{1}{3}$AC=1,∠DEA=$\frac{2π}{3}$,
由余弦定理可知AD2=AE2+ED2-2AE•EDcos$\frac{π}{3}$,
又AC=3,A=$\frac{π}{3}$,则△ABC为直角三角形,
∴a=BC=3$\sqrt{3}$,
∴a的值为3$\sqrt{3}$.
点评 本题考查正弦定理的即余弦定理的应用,考查两角和的正弦公式,考查计算能力,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:解答题
(1)用辗转相除法求228与1995的最大公约数.
(2)用秦九韶算法求多项式f(x)=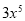 +
+ -8x+5在x=2时的值。
-8x+5在x=2时的值。
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:填空题
直线l1和l2是圆x2+y2=2的两条切线.若l1与l2的交点为(1,3),则l1与l2的夹角的正切值等于________
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{2}{3}$ | B. | $\frac{13}{21}$ | C. | $\frac{13}{7}$ | D. | $\frac{305}{357}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-4,-2] | B. | [-2,6] | C. | [0,8] | D. | [2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com